Escoamento Anular entre Tubos Concêntricos
Produzido por Giovanna RonzéTeoria
Introdução
A ideia agora é trabalharmos com situações em que temos um fluido escoando na região entre duas superfícies cilíndricas, se liga:
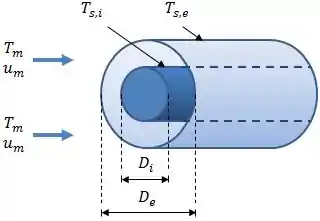
Onde representa a temperatura média do fluido a um ponto qualquer da região anular.
Vamos pensar na seguinte situação:
Água entra na região anular ( e ) a e . A parede do tubo interno é aquecida eletricamente a uma taxa (por unidade de comprimento) de , enquanto a parede do tubo externo é termicamente isolada. A água atinge uma temperatura de na saída dos tubos.
O que queremos responder aqui é o seguinte:
- Qual é a temperatura na superfície do tubo interno na saída, onde condições plenamente desenvolvidas podem ser consideradas?
- O fluxo é positivo se o calor está sendo transferido para o fluido;
- O fluxo é negativo se o calor está saindo do fluido.
A temperatura na superfície interna pode ser calculada da seguinte forma:
Ou seja, precisamos calcular o coeficiente convectivo entre o fluido e a superfície interna.
À temperatura de saída , a água apresenta as seguintes propriedades:
As correlações para o número de Nusselt são divididas para escoamento laminar e escoamento turbulento. Então, antes, precisamos calcular o número de Reynolds.
Para calculá-lo, vamos precisar do diâmetro hidráulico .
Diâmetro hidráulico
Esse cara é definido da seguinte forma:
Para regiões anulares, ele é dado por:
![]()
Substituindo os valores do nosso problema, onde e , teremos:
Agora podemos calcular o número de Reynolds, dado por:
![]()
Onde a área transversal é dada por:
Voltando ao número de Reynolds:
Como , estamos no regime laminar.
Correlações para Escoamentos Anular entre Tubos Concêntricos
Para o escoamento laminar, nós temos duas situações possíveis.
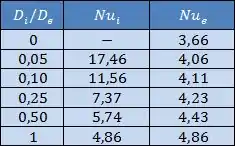
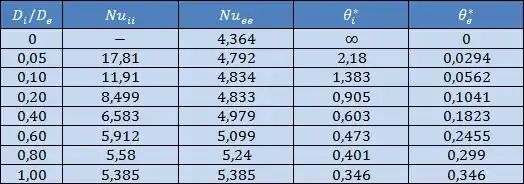
No caso de uma superfície isolada e outra com temperatura constante, os valores para o número de Nusselt para a transferência de calor com a superfície interna e externa são dados na seguinte tabela:
Agora, no caso de fluxo térmico uniforme em ambas as superfícies, os números de Nusselt para as superfícies interna e externa serão dados por:
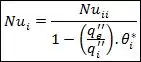
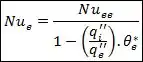
Onde os coeficientes , , e são dados na tabela abaixo:
Se liga! Os fluxos térmicos podem ser positivos ou negativos, de acordo com a seguinte convenção:
Para o escoamento turbulento, podemos usar a seguinte correlação:
![]()
Onde:
- para ;
- para .
Voltando ao nosso problema
No nosso caso, como estamos trabalhando em um escoamento laminar, uma superfície com fluxo térmico uniforme e outra superfície isolada , temos que, para :
Os valores acima foram encontrados fazendo uma média entre os valores para iguais a 0,4 e 0,6.
Substituindo os valores na expressão do número de Nusselt para a superfície interna:
O coeficiente convectivo interno será:
Finalmente, a temperatura da superfície interna na saída da tubulação, será:
![]()
Show de bola! Agora estamos prontos pra cair nos exercícios!
Diâmetro hidráulico D h
Correlações para Escoamentos Anular entre Tubos Concêntricos
Voltando ao nosso problema
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
É prática comum recuperar calor em fornalhas que queimam óleo ou gás através da utilização dos gases de exaustão no preaquecimento do ar de combustão.
Um dispositivo normalmente utilizado para esse propósito é composto por um arranjo de tubos concêntricos no qual os gases de exaustão escoam no tubo interno e o ar de combustão, mais frio, escoa pela região anular.
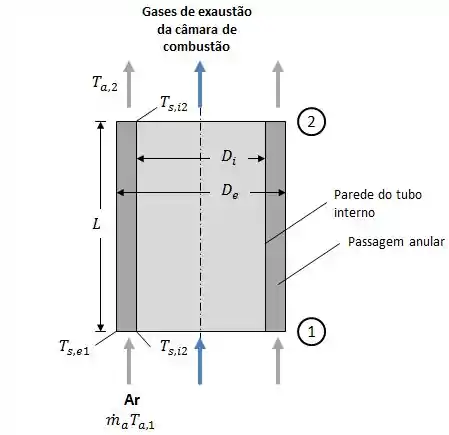
Considere condições nas quais há uma taxa de transferência de calor uniforme por unidade de comprimento do tubo, , dos gases de exaustão para a superfície interna do tubo interno, enquanto o ar escoa pela passagem anular a uma vazão de .
O tubo interno, com parede delgada, tem diâmetro , enquanto o tubo externo, que está isolado da vizinhança, possui diâmetro . As propriedades do ar podem ser consideradas iguais a , , e .
Se o ar entra no arranho a e , qual é a temperatura do ar na saída ?
Se o escoamento do ar é plenamente desenvolvido ao longo de toda a região anular, qual é a temperatura do tubo interno nas seções de entrada e de saída do arranjo? Qual é a temperatura do tubo externo na entrada do arranjo ?
Passo 1
Se o ar entra no arranho a e , qual é a temperatura do ar na saída ?
Como o problema já nos deu as propriedades do ar, podemos determinar a temperatura de saída do ar da seguinte forma:
Substituindo os valores, teremos:
![]()
Passo 2
Se o escoamento do ar é plenamente desenvolvido ao longo de toda a região anular, qual é a temperatura do tubo interno nas seções de entrada e de saída do arranjo? Qual é a temperatura do tubo externo na entrada do arranjo ?
A temperatura superficial é será dada por:
Ou seja, precisamos determinar o coeficiente convectivo pra cada caso, beleza?
Passo 3
Para calcular os coeficientes convectivos, precisamos do número de Nusselt, já que:
Para calcular o número de Nusselt, precisamos do número de Reynolds, dado por:
Onde:
Substituindo os valores:
Opa! Como , estamos no regime turbulento.
Passo 4
Como estamos no regime turbulento, o número de Nusselt será o mesmo tanto para a superfície interna, quanto para a superfície externa, e será dada por:
Substituindo os valores:
Os coeficientes convectivos nas superfícies interna e externa serão:
Agora já podemos determinar as temperaturas que o problema pede.
Passo 5
Como vimos lá no Passo 1, a temperatura de qualquer ponto da superfície é dada por:
- Temperatura do tubo interno nas seções de entrada :
- Temperatura do tubo interno nas seções de saída :
- Temperatura do tubo externo na entrada do arranjo :
Como estamos trabalhando na seção de entrada:
Onde:
Logo:
![]()
Passo 4
Agora, como estamos trabalhando na seção de saída:
Onde:
Logo:
![]()
Passo 5
Como não temos fluxo térmico na superfície externa:
![]()
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Um arranjo de tubos concêntrico, para o qual os diâmetros interno e externo são e , respectivamente, é usado para remover calor de uma reação bioquímica ocorrendo em um tanque de repouso.
Calor é gerado uniformemente no interior do tanque a uma taxa de e uma vazão de de água é alimentada na região anular.
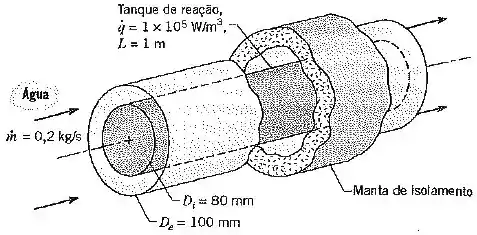
Determine a temperatura de entrada da água vinda do suprimento que irá manter uma temperatura da superfície do tanque média de . Suponha escoamento e condições térmicas plenamente desenvolvidas.
Utilize as seguintes propriedades para a água:
Passo 1
O drama aqui é que não temos nem a temperatura de entrada e nem a de saída , então precisamos dar um jeito de encontra-las.
Bom, a taxa de calor transferida para a água é dada por:
O problema nos deu o calor gerado na superfície interna, e sabemos que a superfície externa é termicamente isolada .
Dessa forma, a taxa de transferência de calor será:
Ao mesmo tempo, podemos associar a taxa de transferência de calor entre o fluido e a superfície interna da seguinte forma:
Onde ..
Opa! Então podemos encontrar a temperatura média reorganizando a equação acima:
Ao encontrarmos a temperatura média, podemos encontrar as temperaturas de entrada e saída reorganizando a primeira equação que vimos:
Ou seja, precisamos do danado do coeficiente convectivo na superfície interna .
Passo 2
Começando pelo número de Reynolds, temos que:
Onde:
Substituindo na expressão do número de Reynolds:
Opa! Estamos no regime laminar! Como estamos trabalhando em um caso onde há fluxo térmico na superfície interna , e uma superfície externa termicamente isolada , temos que:
Logo:
Finalmente, o coeficiente convectivo será:
Passo 3
A temperatura média será:
Passo 4
Agora que já temos a temperatura média, podemos encontrar a temperatura de entrada da seguinte forma:
Substituindo isso na expressão abaixo, teremos:
Agora é só arrumar a bagunça.
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Água, a e , entra em uma região anular formada por uma tubo interno com diâmetro e um tubo externo com diâmetro .
Vapor d’água saturado escoa pelo tubo interno, mantendo a sua superfície a uma temperatura uniforme de , enquanto a superfície externa do tubo externo é isolada.
Se condições plenamente desenvolvidas podem ser admitidas ao longo de toda a região anular, qual deve ser o comprimento do sistema para fornecer uma temperatura de saída da água de ?
Qual é o fluxo térmico saindo do tubo interno na seção de saída do sistema?
Passo 1
O primeiro passo é determinar as propriedades do ar para a média das temperaturas de entrada e saída, dada por:
Assim, de acordo com a tabela A.6 do Incropera, para a água nesta temperatura, temos:
Passo 2
O comprimento do tubo pode ser calculado através da seguinte equação:
Reorganizando o amigão aqui, teremos o seguinte:
Dessa equação, temos praticamente tudo, exceto o coeficiente convectivo. Então vamos atrás dele.
Passo 3
Começando pelo número de Reynolds, teremos:
Onde:
Substituindo os valores:
Como estamos no regime laminar e estamos trabalhando em uma situação onde a temperatura superficial é constante, temos que:
Assim:
Dessa forma, como a superfície externa é isolada, o coeficiente convectivo será:
Passo 4
Agora podemos calcular o comprimento do tubo:
Substituindo os valores, onde :
![]()
Passo 5
O fluxo térmico pode ser calculado da seguinte forma:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Para as condições do problema anterior, qual deve ser o comprimento da região anular se a vazão da água for de ao invés de ?
Passo 1
O comprimento da região anular foi dada pela seguinte equação:
Onde as propriedades do fluido foram as seguintes:
Além disso, temos que:
Passo 2
Ao mudarmos o fluxo mássico, estaremos alterando o número de Reynolds, dado por:
Substituindo os valores:
Agora estamos no regime turbulento, assim o número de Nusselt será dado por:
Substituindo os valores:
Dessa forma, como a superfície externa é isolada, o coeficiente convectivo será:
Passo 3
Agora podemos calcular o comprimento do tubo:
Substituindo os valores, onde :
![]()
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um aquecedor de ar para aplicação industrial é constituído por dois tubos concêntricos, isolados para o lado externo. Nesse sistema o vapor d’água saturado escoa através do tubo central (interior), que tem parede delgada.
Ar escoa através da região anular e a condensação do vapor mantém uma temperatura uniforme de na superfície do tubo.
Considere condições nas quais o ar entra no tubo central, de diâmetro , a uma temperatura de e a uma vazão de , enquanto vapor saturado condensa na superfícies externa do tubo.
Sendo o comprimento do sistema e o diâmetro externo , qual é a temperatura de saída do ar?
Passo 1
Como não sabemos a temperatura de saída, precisamos chutar um valor pra iniciar os trabalhos. Vou chutar uma temperatura de saída de . Nesse caso, as propriedade do ar serão consideradas à temperatura média:
A essa temperatura, o ar possui as seguintes propriedades de acordo com a tabela A.4 do Incropera:
Passo 2
A temperatura de saída pode ser calculada da seguinte forma:
Onde .
Temos tudo nessa equação, menos o coeficiente convectivo. Vamos atrás dele então.
Passo 3
O coeficiente convectivo é dado por:
Para calcular o número de Nusselt, precisamos do número de Reynolds, dado por:
Onde:
Substituindo os valores, teremos:
Assim, o número de Nusselt será:
Finalmente, o coeficiente convectivo será:
Passo 4
Dessa forma, a temperatura de saída será:
Substituindo os valores:
![]()
Nesse caso, vamos parar por aqui, mas se você quiser um resultado mais preciso, a boa é refazer as contas mas usando como chute a temperatura que acabamos de encontrar.
Resposta
Exercício Resolvido #6
Questão 5, PUC, Lista 2
Ao longo do processo de fabricação de barras de chocolate, o chocolate é aquecido usando uma tubulação anular. Vapor saturado escoa na região interna, e o chocolate escoa através da região anular.
O tubo interno tem diâmetro igual a e o tubo externo tem diâmetro igual a , e ambos têm espessura muito pequena. A temperatura da superfície do tubo interno pode ser considerada constante e igual a , e a parede externa do anular está termicamente isolada. de chocolate entram no duto a e devem ser aquecidos até .
Considere o escoamento totalmente desenvolvido e as propriedades do chocolate constantes: . Determine:
O fluxo de calor fornecido ao chocolate.
O coeficiente de troca de calor médio, entre a parede do tubo e o chocolate.
O comprimento necessário para o tubo.
Passo 1
O fluxo de calor fornecido ao chocolate.
O fluxo de calor é dado por:
Substituindo os valores:
![]()
Passo 2
O coeficiente de troca de calor médio, entre a parede do tubo e o chocolate.
Começando pelo número de Reynolds, teremos:
Onde:
Substituindo os valores:
Passo 3
Como estamos no regime turbulento o número de Nusselt será dado por:
Onde o número de Prandtl, por definição, é dado por:
Assim:
Dessa forma, como a superfície externa é isolada, o coeficiente convectivo será:
![]()
Passo 4
O comprimento necessário para o tubo.
O comprimento necessário pode ser calculado da seguinte forma:
Onde a temperatura média é dada por:
Assim, o comprimento será:
![]()
Resposta
Exercício Resolvido #7
Questão 2, UFF, P2-2016.2
Considere um arranjo de tubos concêntricos, para o qual os diâmetros interno e externo são e , respectivamente. O tubo interno é denso e é um reator bioquímico que gera calor a uma taxa de . O raio externo define uma região anular por onde escoa ar.
O conjunto está envolvido por um isolante com condutividade de com de espessura. E todo o sistema está em uma sala a uma temperatura ambiente tal que a superfície externa do isolante esteja a . Qual a vazão de ar necessária para manter a superfície do reator a ?
Admita que o escoamento de ar seja plenamente desenvolvido. As propriedades termofísicas do ar são dadas pelo valor das propriedades a 300K.
Passo 1
De acordo com a tabela A.4 do Incropera, as propriedades do ar a são as seguintes:
Passo 2
Pra calcularmos a vazão de escoamento, precisamos do número de Reynolds, onde:
Para encontrar o número de Reynolds, vamos precisar do número de Nusselt que, supondo escoamento turbulento, é dado por:
Para calcularmos o número de Nusselt, vamos precisar do coeficiente convectivo, dado por:
Finalmente, pra calcular o coeficiente convectivo, como o enunciado nos deu o fluxo térmico, podemos dizer que:
Onde corresponde à temperatura superficial do reator, corresponde à temperatura da superfície externa, e e são as resistências térmicas de condução do isolante e convecção, dadas por:
Ok! Agora vamos colocar isso tudo em prática, indo de trás para frente.
Passo 3
O coeficiente convectivo será dado por:
Isolando o coeficiente convectivo, teremos:
Substituindo os valores, onde :
Obs.: O sinal negativo do coeficiente convectivo se dá pelo fato de que o ar está retirando calor da superfície externa. Na continuação dos cálculos, vamos usar o módulo desse valor.
Passo 4
O número de Nusselt será dado por:
Onde . Logo:
Passo 5
O número de Reynolds será dado por:
Substituindo os valores:
Passo 6
Finalmente, a vazão mássica será dada por:
Onde:
Dessa forma:
![]()