Estado Pseudo-Estacionário
Produzido por Giovanna RonzéTeoria
Nesse tópico a gente vai estudar um caso particular de transferência de massa em que tá rolando estado estacionário e estado transiente ao mesmo tempo.

Calma, jovem. Esse aqui não é muito diferente do que a gente viu antes.
E como é esse tal estado pseudo-estacionário?
Vamos pegar aquele exemplo do tubo com um líquido, onde:
- O líquido contem A
- Tem uma corrente externa de gás de B que não se mistura em A
- O transporte de massa é unidimensional no comprimento do tubo
- Não tem reação química acontecendo.
Nesse caso, o líquido A está evaporando naturalmente. O nível de líquido dentro do tubo vai diminuindo beeem devagarzinho. Então assim, depois de um pequeno período de tempo é como se nada tivesse mudado (estado estacionário), mas depois de um longo período de tempo, a gente vai ter uma queda na altura da interface entre o líquido e o gás (estado transiente), beleza?
Vamos olhar pra esse desenho aqui pra ajudar!
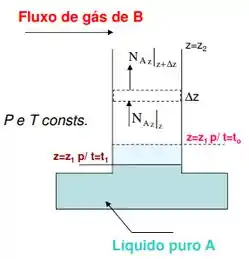
Bom, a gente já viu num modelo bem parecido com esse que:
Onde
E isso serve pra gente descrever o perfil de concentração ao longo do tubo. Então assim, se a gente parasse no tempo e quisesse saber como que estão distribuídas as concentrações ali dentro do líquido em função da altura, é usando essa fórmula ai em cima que a gente acha.
Maaaas, como é que a gente faz pra descobrir quanto tempo que leva pra esse tubo diminuir alguma coisa do nível então?
Fazendo um balanço no tubo, considerando que o fluxo também está relacionado com a quantidade evaporada de A, a gente obtem a seguinte expressão:
Juntando as duas expressões:
Agora separando e integrando em função do tempo:
Com as seguintes condições de contorno:
Finalmente chegamos na seguinte expressão para o tempo:
Agora bora praticar com outros exemplos!
Exercícios Resolvidos
Exercício Resolvido #1
USP - Fenômenos de transporte III - Professor Gerônimo
A célula de Arnold é um dispositivo que, de forma simples, permite a medição de coeficientes de difusão mássica. Na figura a seguir, é mostrado um esboço da célula.
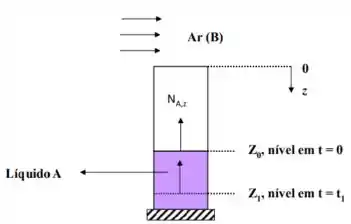
- Determine a difusividade mássica de clorofórmio (A) no ar (B), sabendo que, em um experimento com uma célula de Arnold, em horas (), a distância entre a superfície do clorofórmio e do topo da célula passou de ( ) para ( ). Considere que no topo da célula escoava ar puro, ou seja, , e que na superfície do clorofórmio as condições eram de saturação. A temperatura e a pressão mantiveram-se constantes e iguais a e , respectivamente. A pressão de vapor do clorofórmio nessa temperatura é igual a . Apresente o resultado da difusividade em utilizando o mesmo número de algarismos significativos empregados para representar a distância .
- Qual é a característica do processo que permite a adoção de regime pseudo-estacionário na sua modelagem?
Dados: , ,
Passo 1
Fala aí! Vamos resolver essa questão juntinhos, show? Partiu!
Antes de olhar para todos os dados, vamos começar observando a imagem, beleza?
Temos a célula de Arnold, nela a gente vê um sistema onde o clorofórmio fica dentro de um recipiente aberto, exposto ao ar… Humm… Não temos uma reação química acontecendo, e o fluxo é unidimensional.
A figura também nos indica que primeiro temos uma quantidade de clorofórmio e depois de um certo tempo essa quantidade diminui, indicando uma evaporação, né? Opa! Tudo isso nos permite achar a difusividade pela equação do regime pseudo-estacionário, né? Vamos nessa!!
Agora sim, vamos anotar todos os nossos dados!
Show de bola! Vamos para as continhas!
Passo 2
Bom, lembrando que a equação da difusividade em regime pseudo-estacionário é a seguinte:
Opa! Temos quase tudo, mas ainda tá faltando o , vamos achar ele assim:
Substituindo esses valores, que já foram dados pelo enunciado:
Ficamos então com:
Beleza! Agora vamos achar nossa difusividade! Substituindo nossos valores:
A difusividade será então:
Show!
Passo 3
Agora só falta a letra b, né?
Bom, praticamente respondemos ela no passo 1… haha
O enunciado tá perguntando pra gente qual é a característica desse processo que faz a gente adotar o regime pseudo-estacionário… Olha só, como a gente viu lá no passo 1, temos uma evaporação do clorofórmio que acontece bem devagarinho, e essa taxa de evaporação muito pequena é o que nos indica o regime pseudo-estacionário!
Prontinho! Arrasamos!
Resposta
- A taxa de evaporação muito pequena, do clorofórmio no ar, nos indica o regime pseudo-estacionário.
Exercício Resolvido #2
UFSC - Fenômenos de transporte III - Lista 4 - Professor Bruno Carciofi
Qual a diferença entre difusão em regime permanente e difusão pseudo-estacionária?
Passo 1
Questãozinha teórica só pra gente fixar a teoria, beleza?
Bom, quando temos uma difusão permanente não temos evaporação de uma das espécies, e no caso da pseudo-permanente ocorre evaporação, apesar de ser muito lenta.
Pensa assim, pseudo alguma coisa, quer dizer que é falso, entendeu? Então a difusão pseudo-permanente, nos “engana”, parece uma permanente só que não é, sabe porquê? Se a gente colocar água em um capilar e ficarmos olhando para ele por um tempo curto, vamos achar que não houve evaporação! Mas aí a gente esquece ela lá e vai dar um rolê demorado… Quando voltar, vamos observar que a quantidade de água diminuiu, então houve evaporação!
Pegou o bizu? Show de bola!
Resposta
Na difusão permanente não temos evaporação de uma das espécies, e no caso da pseudo-permanente ocorre evaporação, porém ela é muito lenta.
Exercício Resolvido #3
Fenômenos de transporte III - Professor Gilberto Garcia Cortez
Um capilar está semipreenchido com de etanol. Assume-se que o ar seco contido no interior do capilar esteja estagnado a e . Determine a altura de capilar sabendo que houve um desnível do líquido de no final de .
Dados: ,

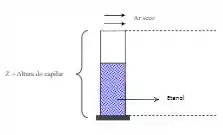
Passo 1
Partiu resolver mais uma questão!
Esse enunciado quer que a gente descubra a altura do capilar () e nos deu os seguintes dados:
Além disso o enunciado da pra gente também uma forma de encontrar o , usando a tabela que foi dada, vamos achar então:
Substituindo os valores:
A pressão será então:
Passo 2
Olha só, pra achar essa altura a gente pode usar a equação do tempo em um regime pseudo-permanente, essa aqui olha:
Tá faltando alguns termos ainda, então vamos descobrir eles:
Substituindo os valores, temos:
Vamos ter então:
E considerando que no topo está presente ar puro, então:
Agora vamos encontrar a concentração que também está faltando:
Usando a constante dos gases como , e substituindo os valores, temos:
A concentração será:
Passando ele para as unidades corretas, vamos ter:
Show! Temos tudo que precisamos, partiu achar o !
Passo 3
Agora vamos voltar lá na equação do tempo e substituir nossos valores:
Ajustando esse cara aí, vamos ficar com:
Conseguimos!!
Resposta
Exercício Resolvido #4
UFSC - Fenômenos de transporte III - Lista 4 - Professor Bruno Carciofi
Propõe-se o seguinte experimento: 4 capilares de 4 cm cada um são mantidos a 25°C e 1 atm, nos quais escoa pelo topo ar seco. Sabe-se que os capilares A, B, C e D contêm, respectivamente, 0,5 cm de benzeno, tolueno, metanol e etanol. Estabeleça uma ordem crescente de tempo, em horas, para o esvaziamento total dos capilares.
Passo 1
Essa questão aqui dá pra gente até pensar em fazer conta, mas no fundo não precisa não! Ela é pra vê se a gente tá ligado!
Bom, temos 4 capilares iguais e com a mesma quantidade de coisa dentro, mas são espécies diferentes, tipo assim, olha só:
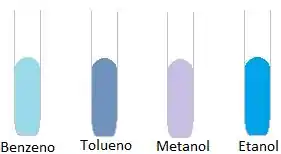
As cores são só pra ilustrar que são composto diferentes, beleza?
Agora vamos dar uma olhadinha na equação que nos ajuda a achar o tempo, pra ver qual o fator nos compostos irão resultar em tempos maiores e menores, ok? Olha ela aqui:
Bom, a densidade e a massa molar deles será diferente, né? Mas o que fará grande diferença mesmo é a massa molar… Então se a gente pensar nela quem tiver a maior massa molar vai ter o menor tempo, certo?
Show! Então vamos anotar a massa molar de cada um:
Como o tempo é inversamente proporcional a massa molar, vamos ter que:
Arrasamos!
Resposta
Exercício Resolvido #5
USP - Fenômenos de transporte III - Professor Gerônimo
Um capilar de de altura contém de etanol. Calcule o tempo necessário para que o nível do álcool decresça em , considerando que o capilar esteja preenchido por ar seco e estagnado a e . Suponha que o vapor de etanol seja totalmente arrastado no topo do capilar. Nessas condições, são conhecidos:
; ; ; Etanol ; Ar seco
Passo 1
Mais uma questãozinha pra fixar nosso conteúdo, beleza? Vamos nessa!
Nesse caso aqui a gente tem um capilar com etanol e com de ar seco, o etanol vai evaporando unidimensionalmente pelo capilar… A gente precisa achar o tempo para que o etanol reduz 0,02 cm de altura… Partiu!
Vamos começar anotando os nossos dados!
Passo 2
Bom, podemos identificar aqui como sendo um regime pseudo-estacionário, e a equação para encontrar o tempo de evaporação é a seguinte:
Ops! Tá faltando gente aí, né? Vamos achar eles! Começando pelo :
Substituindo os valores:
Ficamos então com:
Agora vamos encontrar a concentração assim, olha só:
Usando a constante dos gases, , e substituindo nossos dados:
Teremos:
Para o valor da difusividade do etanol no ar, podemos conseguir pelas tabelas que ficam no apêndice do livro, encontraremos:
Passo 3
Beleza! Agora vamos achar o que nosso enunciado quer! Substituindo nossos valores na equação do tempo, ficamos com:
O tempo será então:
Ou seja, aproximadamente:
Uhul! Arrasamos!
Resposta
Exercício Resolvido #6
Lista de exercício 01 - Transferência de massa - Professora Janaina Karine
Através de uma abertura acidental de uma válvula, água foi espalhada no chão de uma planta industrial em uma área remota de difícil acesso. Estimar o tempo necessário para evaporar completamente a água nas vizinhanças de ar estagnado. A camada de água inicial é de , (que pode ser assumida uniforme) a temperatura de . A pressão parcial de vapor da água nesta temperatura é . O ar está a e . A evaporação é assumida constante e ocorre por difusão molecular através do filme de gás de espessura de . Dados: ;;; .
Passo 1
Fala aí! Vamos ver juntos o que essa questão precisa!
Bom, ela pede o tempo para a água evaporar completamente… Esse problema fala de um vazamento e a água foi derramada no chão, mas o enunciado nos permite considerar como um capilar tendo uma difusão pseudo-permanente, beleza?
Os dados do nosso problema são esses aqui:
Passo 2
Assumindo como sendo um regime pseudo-estacionário a equação que vamos usar para encontrar o tempo de evaporação será essa aqui:
Mas ainda falta coisa aí! Vamos começar achando o :
Substituindo os valores:
Ficamos então com:
Agora vamos encontrar a concentração:
Substituindo nossos dados:
Teremos:
Passo 3
Show de bola! Agora vamos encontrar o tempo!
O tempo será então:
Que louco, né? Vamos passar isso para dias, ok?
Isso significa que vai demorar muitooooo para essa água evaporar… Dá até pra gente considerar que ela não vai evaporar e pedir para alguém secar esse chão, né? hahaha
Resposta
Exercício Resolvido #7
Elaboração própria.
Um capilar é preenchido até a metade de seu comprimento com etanol, com concentração , densidade e coeficiente de difusividade . O ar seco na outra metade do capilar se encontra estagnado, e o etanol leva um tempo, , para evaporar completamente. Como deveria se comportar o tempo, se sua concentração fosse reduzida a metade.
Passo 1
Bom, essa questão aqui quer saber o que acontece com o tempo se a concentração for reduzida a metade… Lembrando que os outros parâmetros serão todos iguais, beleza?
A gente pode fazer a razão da segunda situação, sendo a concentração menor, com a primeira situação… Vamos nessa!
Relembrando que a equação do tempo para um regime pseudo-permanente é:
Vamos ter então nossa razão como sendo:
Cortando todos os termos completamente iguais teremos:
Cortando mais uma vez os termos iguais, temos:
E sendo , ficamos com:
Vamos ficar então:
Isso quer dizer que:
Então se mantemos todos os termos iguais e diminuímos a concentração na metade, o tempo de evaporação vai dobrar, ou seja, uma menor concentração nos oferece um maior tempo de evaporação.
Show de bolinhas!
Resposta
Tendo a metade da concentração, o etanol levará o dobro de tempo para evaporar.
Exercício Resolvido #8
Fenômenos de transporte III - Professor Gilberto Garcia Cortez
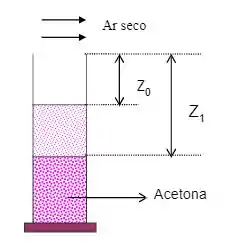
Um capilar contém acetona, cujo nível distancia-se do topo a . O capilar é mantido a e , enquanto que uma corrente de ar seco escoa sobre o topo do tubo. Após de operação, o nível do líquido cai para a mais de corrente de ar. Sabendo que a pressão de vapor da acetona a é , determine o seu coeficiente de difusão no ar seco.
Dado: ;
Passo 1
Fala aí! Vamos resolver esse probleminha aí!
O enunciado quer que a gente descubra coeficiente de difusão no ar seco, e nos deu as seguintes informações:
Pra achar o coeficiente de difusão, podemos usar a seguinte equação:
Opa! Mas tá faltando gente aí, né? Vamos encontrar quem está faltando!
Passo 2
Vamos começar encontrando , assim olha só:
Substituindo os valores, temos:
Vamos ter então:
E considerando que no topo está presente ar puro, então:
Agora encontrando a concentração:
Usando a constante dos gases como , e substituindo os valores, temos:
A concentração será:
Passando ele para as unidades corretas, vamos ter:
Beleza! Agora que temos tudo que precisamos, partiu achar o !
Passo 3
Agora vamos voltar lá na equação e substituir nossos valores:
Vamos ficar com:
Uhul! Show de bola!