Transferência De Calor e Massa
Produzido por Giovanna RonzéTeoria
Fala aí! Hoje vamos aprender um pouquinho melhor sobre Transferência de Calor e Massa.
Já parou pra estudar uma matéria da sua faculdade pelo livro que seu professor recomendou e não sabia nem por onde começar? O Responde Aí tá aqui pra pegar sua mão e te mostrar o caminho!
Inclusive, vou deixar aqui embaixo alguns links que podem complementar muito bem o que veremos nessa página. Não deixa de conferir o primeiro, com todos os exercícios do livro do Incropera resolvidos passo a passo!
⭐ Veja também ⭐
- Incropera - Fundamentos de Transferência de Calor e de Massa - 7a Edição Resolvido Passo a Passo.
- Difusão sem reação química.
- Introdução à Condução e Lei de Fourier.
- Introdução à Convecção.
Como ocorre a Transferência Simultânea de Calor e Massa?
Nos processos industriais reais, as transferências de calor e de massa ocorrem ao mesmo tempo. Uma reação química qualquer é um exemplo claro disso, concorda? As reações geram ou consomem calor, ao mesmo tempo em que há a reorganização dos elementos químicos.
Por causa disso, é importantíssimo aprender a modelar matematicamente os sistemas que transportam calor e massa de maneira simultânea.
A transferência de calor é o processo que ocorre quando dois corpos de temperaturas diferentes são aproximados. O calor do corpo de maior temperatura é transmitido para o de menor até que eles atinjam temperaturas iguais.
Já a transferência de massa, é o processo de transporte de espécies químicas de uma região para outra. Isso se dá pelos mecanismos de difusão ou convecção.
E como esses caras ocorrem simultaneamente? Ora, quando uma substância está se difundindo, ela também difunde sua energia interna. Isso é mostrado por essa expressão aqui:
👉
👉
👉
👉
Agora, se tiver um gradiente de temperatura aí nesse meio, devemos somar a Lei de Fourier para condução:
Aquele
Masss, quando o fluido está em movimento, a transferência de calor é dada pela convecção. Aí a equação passa a ser essa aqui:
E o
Transferência de Calor e Massa com Mudança de Fase
Essa imagem aqui ilustra a condensação de um gás em uma superfície fria:
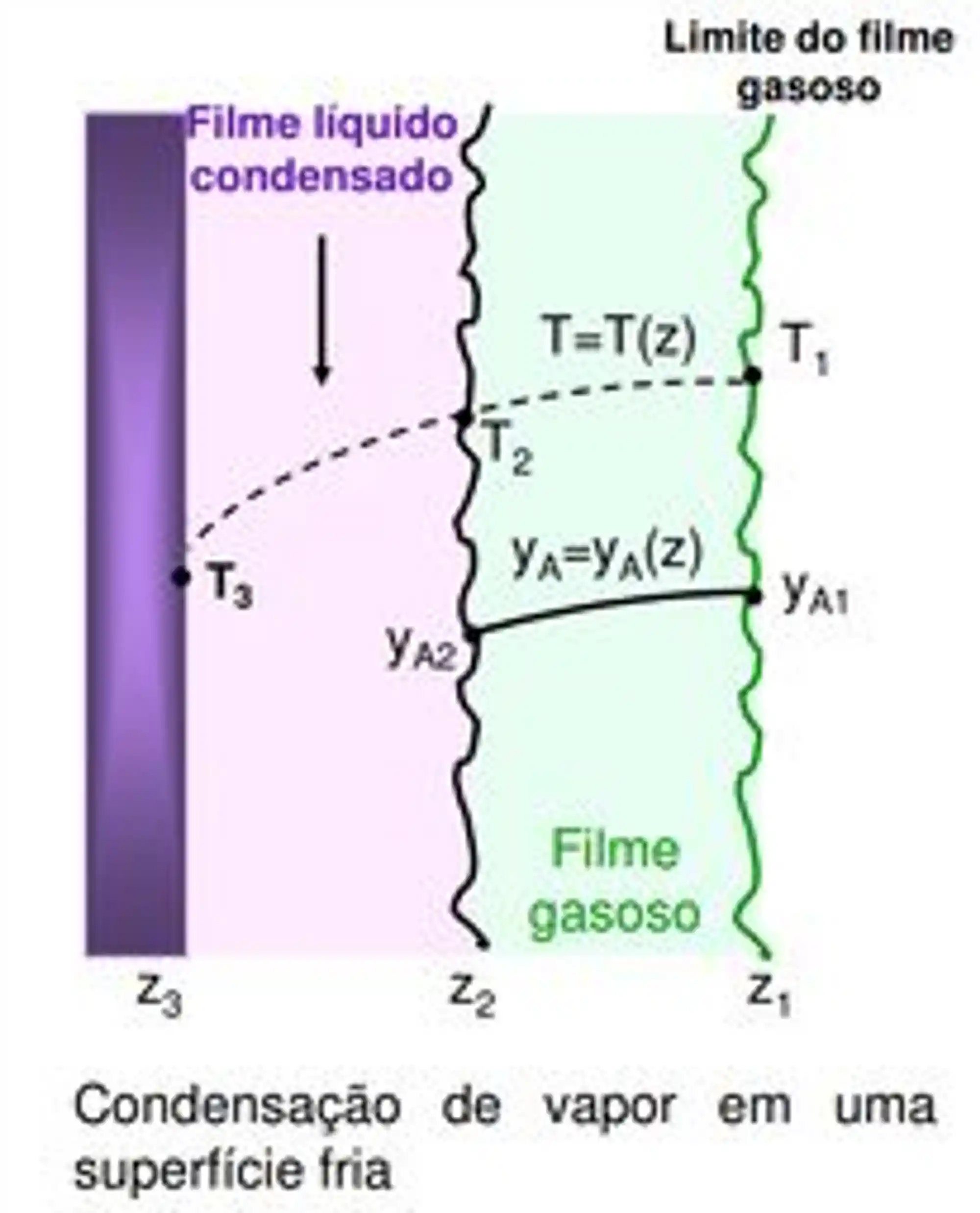
Vamos considerar que somente A está condensando, não há reação química e o transporte de calor e de massa é só na direção do eixo z.
Pelas correlações de transferência de calor, é possível calcular o coeficiente de convecção:
Esse
Para a transferência de massa, vamos usar um balanço diferencial:
Se usarmos a expressão do fluxo para A difundindo, chegamos nisso aqui:
Como a temperatura está mudando ao longo do eixo, a gente tem que achar uma correlação entre a difusividade e z. Se liga nisso aqui:
Supondo um perfil de temperatura, a gente pode escrever assim:
E como estamos falando de gases, temos essa relação aqui:
Aí a expressão do fluxo fica:
Para resolver essa expressão, usamos as condições de contorno:
Com isso, o fluxo de energia total vai ser expresso assim:
Belezinha? Bora praticar um pouco com nossos exercícios selecionados pra você então!
Transferência de Calor e Massa com Mudança de Fase
Exercícios Resolvidos
Exercício Resolvido #1
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Considere um raso corpo de água. É possível que a água congele durante uma noite fria e seca, mesmo se o ar ambiente e a temperatura da superfície em torno nunca chegar a ? Explique.
Passo 1
Questãozinha teórica que a gente gosta pra fixar os conhecimentos que adquirimos até aqui!
Bom, o enunciado quer saber se um pouquinho de água exposto durante a noite pode congelar, mesmo que a superfície não atinja a temperatura de , que é a temperatura de congelamento da água em uma pressão atmosférica…
Bom, a primeira coisa que poderia passar pela nossa cabeça é que isso não é possível, né? Mas vamos analisar com calma e usando todo nosso conhecimento de transferência de calor e massa, ok?
Pensa só, se o ar em volta do corpo de água não estiver saturado vai ter uma transferência de massa ali, né?
E para isso acontecer então nossa água que estava líquida precisa evaporar, certo?

Como é que a água vai evaporar se o ar e a superfície dela estão na mesma temperatura? De onde vai vir essa energia?
Passo 2
Vamos nos esforçar pra entender isso, beleza?
É o seguinte, sabe a água de está mais no interior do corpo de água? Então, ela vai ceder energia para que a água da superfície possa evaporar… Beleza?
E se ela está perdendo energia, o que vai acontecer com ela????

Exatamenteee!! A porção de água do interior vai perder energia para a evaporação da água da superfície e assim consegue atingir a temperatura de congelamento!
Opa! Então nossa resposta é sim!!!
Resposta
Sim, é possível que a água congele, caso ocorra uma transferência simultânea de calor e massa.
Exercício Resolvido #2
Adaptado de Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Em um dia de verão, quando a temperatura marca cerca de , a , precisamos resfriar uma lata de refrigerante. Para fazer isso vamos manter um continuamente molhado em volta da latinha e colocá-la em frente a um ventilador. Considerando uma umidade relativa de , determine a temperatura da bebida quando as condições permanentes forem atingidas.
Passo 1
Bom, vejamos o que temos aqui… O ar sai do ventilador direto para uma latinha embrulhada em um pano úmido… Hummm… Estamos então tentando esfriar ela por transferência simultânea de calor e de massa, certo?
O enunciado deu pra gente a temperatura, a pressão e a umidade relativa do ar… Mas pra seguir em frente precisamos fazer algumas considerações, ok?
Vamos primeiro desprezar os efeitos da radiação e depois considerar o ar e o vapor d'água como gases ideais… Agora sim vamos partir para achar o que o problema quer.
Passo 2
Agora vamos visitar a tabela A-9 e A-15, para pegar alguns dados da água e do ar seco, ok? Mas para isso precisamos de uma temperatura média, então vamos encontrar ela assim:
Ops! Temos o , mas não temos a temperatura da superfície… Então vamos considerar uma, tranquilo? Vamos supor que:
Agora sim podemos ter uma temperatura média, e ela será:
Agora sim, visitando as tabelas, temos como dados adicionais para a água:
Opa! Mais ainda está faltando um dado importante para a água, o valor de na temperatura de , ele será:
Agora sim, vamos as propriedades do ar seco:
Agora olhando para a tabela A-1, temos as massas molares deles sendo:
E visitando a tabela 14-4, temos a difusividade do vapor de água no ar a , como sendo:
Passo 3
Beleza! Agora que reunimos todos os dados possíveis, vamos achar a temperatura! Para isso podemos usar a equação de Chilton-Colburn, que diz:
Xiii! Deu ruim! Tá faltando gente ali ainda pra gente calcular a temperatura… Vamos começar calculando o número de Lewis, ok?
Nós temos esses dados, então substituindo:
Teremos então:
Agora precisamos encontrar a pressão de vapor na superfície… E como nós temos o ar da superfície saturado ela vai ser igual a pressão de saturação da água na temperatura da superfície:
E a pressão de vapor do ar distante da superfície será:
Teremos então:
E substituindo nossos valores:
Ficaremos com:
E não podemos esquecer, que a pressão dada foi de:
Passo 4
Uhul! Agora sim temos todos os dados, vamos voltar lá na nossa equação da temperatura:
Substituindo nossos valores:
E temos como a temperatura da bebida na superfície sendo:
Prontinho! Arrasamos!!
Resposta
Exercício Resolvido #3
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Durante a evaporação a partir de um corpo de água para o ar, em que condições o calor latente de vaporização é igual à transferência de calor por convecção do ar?
Passo 1
Fala aí! Partiu resolver essa questão aí juntos! O enunciado quer saber qual a condição que o calor latente de vaporização vai ser igual a transferência de calor por convecção, certo?
Bom, no comecinho da evaporação temos uma taxa de evaporação maior que o calor que é fornecido pelo ambiente, certo? Sendo assim, então, o corpo de água vai cedendo energia para a evaporação continuar… E fazendo isso a temperatura dele vai diminuir!
Mas chega um momento em que esse sistema vai entrar em regime permanente, e aí a temperatura do corpo de água vai estabilizar, teremos então um equilíbrio térmico. Nessa condição vamos ter que o calor latente de vaporização será o mesmo que a transferência de calor por convecção, belezinha?
Show de bola!
Resposta
Passo 1.
Exercício Resolvido #4
Fundamentos da transferência de calor e massa - 7ª Edição - Incropera e Dewitt
Considere a difusão de hidrogênio (espécie A) em ar, em água líquida ou em ferro (espécie B), a . Calcule os fluxos da espécie nas bases molar e mássica, se o gradiente de concentração em um local específico for igual a . Compare o valor da difusividade mássica com o da condutividade térmica. A fração molar do hidrogênio, , é muito menor que um.
Passo 1
Vamos lá! Nesse problema precisamos do fluxo mássico e do fluxo molar do hidrogênio e também precisamos encontrar os valores de difusividade térmica e mássica para as três espécies pedidas, ok?
Vamos começar buscando dados auxiliares, esses dados podem ser encontrados no apêndice do livro que você usa na matéria, beleza?
Para o hidrogênio e o ar, vamos ter:
Para o hidrogênio e a água:
Para o hidrogênio e o ferro:
Além das difusividades, precisamos de mais alguns dados, no caso do ar:
No caso da água:
E para o ferro:
Passo 2
Agora podemos encontrar a difusividade mássica do hidrogênio em cada espécie, na temperatura de , usando a relação:
Primeiro para o ar:
Agora para a água:
E para o ferro:
O enunciado nos disse que a fração molar do hidrogênio é muito menor que um, isso quer dizer que estamos trabalhando com uma espécie diluída e por conta disso a difusividade térmica da água pode ser dada por:
Passo 3
Beleza! Estamos quase lá! Agora vamos encontrar o fluxo molar, para cada uma das espécies, ok? Podemos encontrá-lo assim:
E lembrando que o enunciado nos deu que … Vamos ter para o ar:
Para a água:
E para o ferro:
Para fechar vamos achar o fluxo mássico de cada espécie, com a relação:
Para o ar, vamos ter:
Para a água:
E para o ferro:
Conseguimos! Vimos aqui que diferentes materiais respondem à transferência de massa com taxas bem distintas, dependendo se o meio será um gás, no caso do ar, um líquido, no caso da água, ou um sólido, no caso do ferro.
Resposta
Para o ar:
Para a água:
Para o ferro:
Exercício Resolvido #5
Adaptado de Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Marque as declarações como sendo verdadeiras (V) ou falsas (F).
- As unidades da difusividade da massa, da difusividade térmica e da difusividade da quantidade de movimento são todas iguais.
- Se a concentração molar (ou densidade molar) C de uma mistura é constante, então sua densidade também deve ser constante.
- Se a velocidade média da massa de uma mistura binária é igual a zero, então a velocidade média molar da mistura deve também ser zero.
- Se as frações molares de A e B em uma mistura são, ambas, de 0,5, então a massa molar da mistura é simplesmente a média das massas de A e B.
Passo 1
Vamos juntos analisar cada uma dessas afirmações!
Começando pela letra a, a unidade das difusividades térmica, de massa e de movimento são, no S.I. , logo essa afirmação é verdadeira!
Agora analisando a letra b, a densidade não depende apenas da concentração molar, por isso mesmo a concentração sendo constante, não quer dizer que a densidade será também. Portanto, essa é falsa!
A letra c, diz que se a velocidade da mistura binária for zero, a velocidade média molar da mistura também vai ser, mas para isso acontecer as frações molares devem ser iguais, senão isso não é real. Sendo assim, a alternativa é falsa, pois não será necessariamente assim, beleza?
Para fechar vamos de letra d, analisando a massa molar da mistura é dada pela soma da fração molar multiplicada da massa molar de cada espécie da mistura… Então se cada uma tem a mesma fração molar a massa molar da mistura será sim a média das massas. Portanto, é verdadeira!
Pronto! Conseguimos!
Resposta
- V
- F
- F
- V
Exercício Resolvido #6
USP - Transferência de massa - aula 09 - Professor Gerônimo.
O diclorometano é um ingrediente comum em decapantes de tintas. Além de causar irritações, pode ser absorvido pela pele. Deve-se usar luvas de proteção quando manipular este decapante. Usando-se luvas de borracha butílica ( de espessura), qual é o fluxo de diclorometano através da luva?
Dados: Coeficiente de difusão em borracha butílica:
Concentrações superficiais: e
Passo 1
Fala aí! Olha só um probleminha comum em transferência de massa! Precisamos encontrar o fluxo mássico de diclorometano através das luvas, ok? Vamos nessa!!
Podemos achar o fluxo usando a equação:
Essa variação ficará com a seguinte cara:
E sendo esse delta a diferença entre final e inicial, teremos:
Beleza! Substituindo os dados do nosso enunciado:
Ficaremos então com um fluxo de:
Prontinho!
Resposta
Exercício Resolvido #7
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Jarras feitas de argila porosa foram comumente utilizadas para resfriar água no passado. Uma pequena quantidade de água que vaza para fora mantém a superfície externa do jarro molhada o tempo todo, e o ar relativamente seco e quente fluindo sobre a jarra causa a evaporação dessa água. Parte do calor latente de evaporação provém da água na jarra e, como resultado, a água é resfriada. Considerando que as condições ambientais são , e de umidade relativa, determine a temperatura da água quando as condições permanentes forem atingidas.
Passo 1
Bom, vamos para mais uma questãozinha! O bizu dessa aqui, é lembrar que quando estamos em condições de regime permanente temos que o calor latente de vaporização é igual a transferência de calor por convecção, beleza?
Pra começar, a gente precisa da temperatura da superfície que não temos… Vamos então supor que temos:
Nessa temperatura, vamos ter as seguintes propriedades da água:
Agora, trabalhando com a temperatura média, vamos ter:
Substituindo nosso dado, com a temperatura que a gente supôs:
Vamos ter então:
Na temperatura média, as propriedades do ar são:
E ainda na temperatura média, temos a difusividade do vapor de água sendo:
Lembrando que todos esses dados são tabelados, de acordo com a temperatura que estamos usando, ok?
Passo 2
Agora sim! Vamos usar a equação para encontrar a temperatura da superfície, no caso de transferência simultânea de calor e massa:
Ops! Tá faltando coisa aí ainda, hein? Vamos começar pelas pressões… Estando o ar a uma temperatura de , que foi dado no enunciado, temos a pressão de vapor da água:
E sendo a pressão parcial do vapor de água na fase gás, dada pela equação:
Vamos ter então:
Usando a umidade relativa dada no enunciado e o valor da pressão de vapor, vamos ficar com:
E teremos a nossa pressão sendo:
Show! Agora só falta achar o número de Lewis! Vamos nessa!
Temos esses dados, substituindo ficamos com:
Passo 3
Partiu calcular a temperatura! Relembrando que:
Lembrando que temos as massas molares serão:
E agora substituindo os valores que foram dados e os que encontramos, temos:
Nossa temperatura será, aproximadamente:
Resposta
Exercício Resolvido #8
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Uma piscina aquecida de X e de profundidade é mantida a uma temperatura constante de em um local onde a pressão atmosférica é . Considerando que o ar ambiente está a , a umidade relativa é e a temperatura efetiva do céu é . Determine a taxa de perda de calor a partir da superfície superior da piscina por (a) Radiação (b) Convecção e (c) Evaporação. (d) Considerando as perdas de calor para o chão desprezíveis, determine o tamanho do aquecedor.
Passo 1
Fala aí! Parece que essa questão vai nos dar trabalho, né? Mas relaxa que tamo junto e vai dar certo!
Vamos começar anotando nossos dados, beleza?
Com esses dados aí a gente precisa achar a taxa de perda de calor por radiação, convecção e evaporação e com esses resultados encontrar o tamanho do aquecedor… Partiu!
Passo 2
Para encontrar a taxa de transferência de calor por radiação, vamos usar a seguinte equação:
Lembrando que , vamos ficar com:
Teremos uma taxa de radiação igual a:
Passo 3
Agora vamos buscar a taxa de transferência de calor por convecção, ok? Para isso vamos usar a equação:
Ops! Quem é esse ? Precisamos encontrar ele! Vamos nessa! Pra começar, temos que achar uma temperatura média e buscar alguns dados adicionais, ok?
Vamos ter:
Bom, com essa temperatura temos as seguintes propriedades para o ar:
E com esses dados adicionais a gente pode achar o número de Rayleigh:
Substituindo nossos dados:
O número de Rayleigh será então:
Com ele a gente encontra o número de Nusselt:
E agora sim podemos encontrar o coeficiente convectivo! Ufaaa! Usando essa relação aqui:
Vamos ter, nosso coeficiente como sendo:
Substituindo os valores:
Ficaremos com:
Show! Nosso calor de convecção será:
Passo 4
Agora é a vez da taxa de calor por evaporação, vamos lá! Ela pode ser encontrada usando a seguinte equação:
Eita! Não temos nenhuma das propriedades! Relaxa! No caso da entalpia de vaporização da água, ela é tabelada e na temperatura de , será:
Mas precisamos da taxa mássica! Para achar ela vamos começar usando a seguinte relação:
Isolando o que queremos, ficamos com:
Usando as propriedades do ar, para a temperatura de , vamos ter que:
Sendo assim, ficaremos com:
Agora que chegamos até aqui, vamos buscar a taxa molar de transferência de massa, por essa equação:
Vish! Não temos nem a concentração, nem as frações molares de água na superfície da piscina e no ar… Vamos calcular isso então!
Podemos achar a concentração assim:
Substituindo nossos dados, ficamos com:
Beleza! E a nossa fração molar podemos usar a equação:
E considerando que o ar na superfície está saturado, então , e como a umidade relativa é de , temos que , sendo assim ficamos com:
Sendo a pressão de vapor da água , a , e sendo , a , podemos achar que:
E para o ar:
Aeee! Agora vamos achar a transferência de massa, como sendo:
Agora vamos transformar isso em taxa mássica, assim olha só:
E finalmente podemos encontrar a taxa de evaporação:
Passo 5
Opa! Agora só falta encontrar a potência do nosso aquecedor… estamos quase lá!
A potência será dada assim:
Substituindo os valores que encontramos:
Ficaremos com:
Enfim, Conseguimos!