Força de Sustentação
Produzido por Raphael EloiTeoria
Introdução
E ae! Dominou tudo de arrasto? Bora entender agora essa tal de sustentação.
A gente já viu que, quando o fluido entra em contato com uma superfície, surgem as tais forças de arrasto () e de sustentação (). Qualquer objeto que estiver se movendo num fluido vai estar sujeito a essas forças.
Você lembra do conceito de linhas de corrente? As linhas de corrente são uma forma de representar o campo de velocidades do escoamento. E a gente já aprendeu que, quanto maior o número de linhas de corrente numa região, maior é a velocidade do fluido nessa região.
Beleza! Mas, pela equação de Bernoulli, quanto maior a velocidade em um certo ponto, menor a pressão nesse mesmo ponto (fixada uma altura ):
Então, o que a gente pode concluir? Quanto maior a concentração de linhas de corrente numa região, maior será a velocidade e menor será a pressão nessa região.
Nas situações em que o objeto é simétrico e seu posicionamento em relação ao fluido gera linhas de corrente simétricas, não existe diferença de velocidade entre a parte de cima e a parte de baixo e, consequentemente, não existe diferença de pressão. Dá uma olhada nesses exemplos:
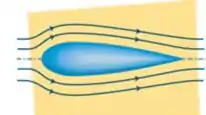
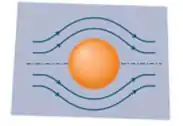
Mas esses casos são muito específicos, não é mesmo? É normal vermos situações nas quais existe um ângulo de inclinação do objeto ou simplesmente situações nas quais o objeto não é simétrico, como por exemplo:
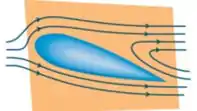

Nessas imagens, dá pra perceber que as linhas de corrente na região acima do objeto são diferentes das que a gente vê na parte de baixo. Então, se tem diferença no campo de velocidades, tem diferença na pressão entre essas regiões. Essa diferença de pressão resulta na força de sustentação ().
Resumindo, temos o seguinte sistema:
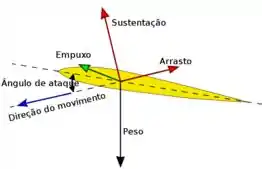
Na imagem, a gente consegue visualizar uma situação genérica, na qual existe:
- Força de Arrasto (na mesma direção do escoamento),
- Força de Sustentação (perpendicular ao escoamento).
OBS: O empuxo não é nosso foco nesse tópico, pequeno gafanhoto, mas já estudamos essa força! ^^
Coeficiente de Sustentação
Assim como na força de arrasto a gente viu uma forma de caracterizar a geometria dos objetos por meio de um coeficiente (), para a força de sustentação, a gente usa o coeficiente de sustentação (). Ele é definido matematicamente como:
A expressão é bem parecida com a de, não é mesmo? A diferença é que temos a força de sustentação no numerador e a área () aqui se refere à área projetada na direção perpendicular ao escoamento. Para o exemplo de um aerofólio como mostrado abaixo, a área projetada () é dada pelo produto:

Ângulo de ataque
A gente viu anteriormente que a inclinação do objeto em relação ao escoamento altera o a força de sustentação. Essa inclinação pode ser medida pelo que chamamos de ângulo de ataque (), que é o ângulo do corpo em relação à direção do escoamento.
O comportamento do coeficiente de sustentação em função do ângulo de ataque obedece ao seguinte gráfico:
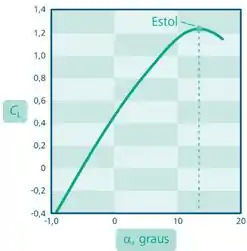
Observe que o gráfico tem regiões:
- Antes do estol: ao aumentar a inclinação do objeto em relação ao eixo do escoamento, o coeficiente de sustentação também aumenta.
- No valor de estol: maior valor do coeficiente de sustentação e, consequentemente, ponto onde a força de sustentação () é máxima.
- Depois do estol: ao aumentar ainda mais o ângulo de ataque, o coeficiente diminuirá.
A velocidade de estol pode ser calculada por essa fórmula:
Sendo P a força peso e o coeficiente de sustentação máximo, que pode ser obtido pelo gráfico a depender do ângulo de ataque e da geometria
Com isso, quando se quer projetar algum dispositivo, é importante conhecer bem o sistema e prever a qual ângulo o objeto será submetido para que nada saio do controle! Sentiu a responsa? hahaha
Bora fixar o que a gente aprendeu agora! Então, responde aí! ^^
Coeficiente de Sustentação
Ângulo de ataque
Exercícios Resolvidos
Exercício Resolvido #1
VILANOVA, L. C. Mecânica dos Fluidos. Colégio Técnico Industrial de Santa Maria, RS. 2011.
(Adaptada) Considerando um projeto de aeronave que deva voar com velocidade constante e igual a numa mesma altitude e que tenha uma asa com comprimento de e largura de , determine o coeficiente de sustentação e a carga da asa. Admita que a massa do avião com o piloto é de .
OBS: Somente a asa do avião é responsável pela sustentação e a carga da asa é definida como a razão entre a força de sustentação e a área projetada.
Passo 1
Avaliando o sistema, para que o avião permaneça em voo, a força resultante vertical deve ser nula e, consequentemente, a força de sustentação () deve se igualar à força peso ():
Dessa maneira, isolando o coeficiente de sustentação ():
Substituindo os valores informados no enunciado, temos:
Passo 2
Como foi informado no enunciado, a carga da asa é dada pela razão entre a força de sustentação () e a área projetada da asa ():
Então, primeiro podemos calcular a força de sustentação da seguinte maneira:
Resposta
Exercício Resolvido #2
VILANOVA, L. C. Mecânica dos Fluidos. Colégio Técnico Industrial de Santa Maria, RS. 2011.
Uma bola de tênis lisa, com massa de e de diâmetro, é golpeada na sua parte superior (topsipin) a , o que lhe confere uma rotação de . Calcule a sustentação aerodinâmica atuando sobre a bola. Avalie o raio de curvatura da sua trajetória na máxima elevação do plano vertical. Comapre com o raio quando não houver rotação.
(Dados: e )
Passo 1
Bom, vamos lá! Esse problema se relaciona com o que chamamos de efeito Magnus. O efeito Magnus ocorre quando um corpo, além de se mover em uma direção, roda em torno de seu próprio eixo. Dá uma olhada aqui em baixo:
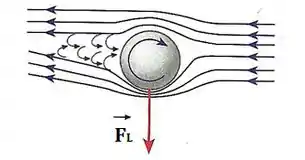
Observe que ao golpearmos a bola de tênis na parte superior, ela apresentará determinada rotação (sentido horário) além de se mover para frente. Então, a gente percebe que:
- Na parte de cima: a velocidade da superfície da bola tem sentido oposto ao escoamento do ar.
- Na parte de baixo: a velocidade da superfície da bola tem mesmo sentido que o escoamento do ar.
Dessa forma, o fluido na parte de cima é desacelerado e o fluido na parte de baixo é acelerado, surgindo, assim, regiões com diferentes velocidades e, consequentemente, regiões com diferentes pressões.
Como a velocidade na parte superior é menor que a velocidade na parte inferior, logo a pressão em cima será maior que a pressão em baixo, gerando uma força de sustentação de cima para baixo ().
Bacana! A gente já viu como calcular a força de sustentação:
A área da projeção () será a área do círculo de diâmetro igual ao da esfera ():
Substituindo os valores de cada grandeza, teremos:
Passo 2
Como vimos, a bola é atingida na parte de cima e “ganha rotação” no sentido horário, resultando numa força resultante para baixo. Usando a segunda lei de Newton para avaliar a curvatura da trajetória no plano vertical temos:
Lembre-se de que a aceleração centrípeta () é dada por:
Substituindo a expressão na equação, teremos:
Então, dividindo a equação por e isolando o raio (), temos que:
Passo 3
Se não houvesse rotação, as linhas de corrente seriam simétricas e a gente não verificaria diferenças de pressão. Logo a componente da força de sustentação () seria zero! Consequentemente a expressão do raio seria dada por:
Concluimos, portanto, que há diferença entre as situações com rotação e sem rotação, logo o efeito Magnus é importante!
Resposta
A força de sustentação calculada foi de:
Os valores do raio calculados na situação com rotação () e sem rotação () são respectivamente:
Exercício Resolvido #3
PINHO, F. T., Guia de Apoio em Mecânica dos Fluidos. Seção de Escoamentos Exteriores.
(Adaptada) Um avião Piper tem uma massa de e voa com um a velocidade de . Sabendo que a área da superfície projetada é de , determine o coeficiente de sustentação nessas condições e a potência requerida pelo motor, sabendo que o coeficiente de arrasto () equivale a .
Passo 1
Primeiro passo nosso será encontrar o coeficiente de sustentação (). Para que o avião permaneça voando na mesma altitude, a componente vertical da força deve ser zero. Como só atuam a força peso e a força de sustentação, temos que:
Substituindo a nossa velha conhecida expressão para , temos:
Antes de prosseguirmos, vamos converter a velocidade para o S.I.:
Substituindo as informações do problema:
Logo:
Passo 2
Agora, vamos ao cálculo da potência! “Mas que potência é essa?” Ela é a energia que o motor do avião precisa fornecer por unidade de tempo, para que ele se locomova.
A gente sabe que o escoamento de objetos está sujeito às forças viscosas e, por isso, existe uma resistência ao deslocamento. Essa energia é a que o avião precisa para vencer a resistência relativa ao arrasto.
Podemos escrever a potência () como a razão entre o trabalho da força pelo tempo:
Como a razão entre a distância e o tempo é a própria velocidade do avião, temos que:
Como a força que tratamos aqui é a força de arrasto (), podemos escrever:
Substituindo o coeficiente de arrasto () e os demais valores do enunciado:
Resposta
Exercício Resolvido #4
PINHO, F. T., Guia de Apoio em Mecânica dos Fluidos. Seção de Escoamentos Exteriores.
(Adaptada) Um Boeing 747, que pesa com combustível, leva passageiros e decola a uma velocidade de . O peso médio de cada passageiro com sua mala é igual a . Calcule a velocidade que o Boeing deve ter para decolar quando carregar passageiros (com suas respectivas bagagens).
Assuma que a configuração geométrica e o ângulo de ataque são os mesmos em ambas situações.
Passo 1
E aí! Já pensou como resolver esse problema, pequeno gafanhoto? O enunciado nos pede a velocidade do Boeing quando carrega um número diferente de passageiros. O que isso indica? Indica que a massa do corpo vai mudar!
Você percebeu que nos foi pedido para assumir que a configuração geométrica e o ângulo de ataque são os mesmos? Pois é! Isso tá falando pra gente indiretamente que o coeficiente de sustentação não varia de uma situação para outra, já que ele só depende disso.
Beleza, então vamos primeiro avaliar a situação I (com passageiros). Para que o avião permaneça na mesma altitude em seu voo, precisamos que a força resultante na direção vertical seja nula e, matematicamente, isso quer dizer que:
Substituindo expressão para , temos:
Antes de prosseguirmos, vamos calcular a massa total () do sistema:
Em que representa o número de passageiros. Sendo assim:
Antes de prosseguirmos, bora converter a velocidade para o S.I.:
Substituindo as informações do problema:
Mas e a área? Não nos foi dada nenhuma informação quanto à geometria do problema! Calma, mestre. Realmente não sabemos qual a área do avião, mas sem desespero! A gente sabe que essa área é a mesma na situação II (com passageiros). Então, o produto vai ser igual em ambas situações e ele vale:
Beleza! Não sabemos quem é o coeficiente de arrasto () nem a área (), mas só precisamos conhecer o valor do produto entre eles, já que é o mesmo que vamos usar na situação II a seguir. :)
Passo 2
Na situação em que o Boeing carrega passageiros com suas respectivas bagagens, a massa total do sistema será:
Como as condições geométricas são as mesmas, podemos escrever que:
Logo:
Isso equivale a , ou seja, é um aumento de quase 3%. Muito pouca a diferença, não é mesmo? E olha que colocamos pessoas a mais nesse Boeing!
A diferença é pequena, pois a contribuição da massa do avião com combustível é muito maior que a contribuição da massa dos passageiros.
Resposta
Exercício Resolvido #5
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 526, ex. P 7.115
O jato executivo Cessna Citation pesa 67 kN e tem uma área de asa de 32 m². O jato voa em condição de cruzeiro a 10 km de altitude padrão com um coeficiente de sustentação de 0,21 e um coeficiente de arrasto de 0,015. Calcule (a) a velocidade de cruzeiro em km/h e (b) a potência em hp necessária para manter a velocidade de cruzeiro.
Dados:
Passo 1
Nesse exercício temos o jato voando a uma altitude constante. Então, no eixo y, o somatório de forças é igual a zero.
As forças atuando no eixo y são a força peso e sustentação. A força peso aponta para baixo e a de sustentação para cima. Então:
Vimos na teoria que a força de sustentação é:
A área corresponde a área de asa. Substituindo os valores dados no enunciado:
Convertendo para km/h
Essa é a velocidade de cruzeiro. 😊
Passo 2
Uma das formas de encontrar a potência é multiplicando a força pela velocidade. Mas, tem um detalhe importante! Aqui vamos utilizar a força de arrasto, pois é ela que propicia o movimento, que está acontecendo no eixo x.
No tópico anterior, vimos que a força de arrasto é
Substituindo o coeficiente de arrasto , e as outras variáveis:
Encontramos a potência necessária para manter a velocidade de cruzeiro =D
Resposta
Exercício Resolvido #6
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 526, ex. P 7.116
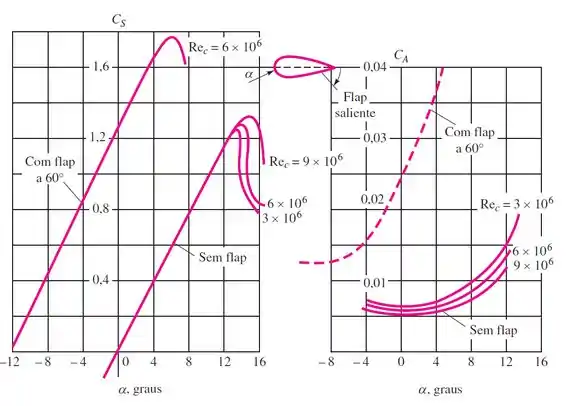
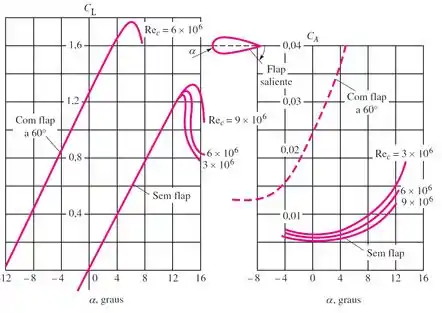
(Adaptada) Um avião pesa 180 kN e tem uma área de asa de 160 m² e uma corda média de 4 m. As propriedades de aerofólio são dadas pela figura. Se o avião é projetado para pousar a , usando um flap saliente (split flap) colocado a 60°, qual é a velocidade de aterrissagem apropriada em km/h?
Dados:
Passo 1
Para calcular a velocidade de aterrisagem , vamos precisar conhecer a velocidade de estol. Como vimos na teoria, a velocidade de estol é
Conhecemos o peso e a área projetada. Para encontrar o coeficiente de arrasto máximo , vamos usar o gráfico fornecido no enunciado.
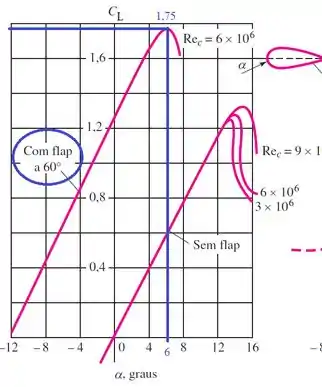
Pela curva do aerofólio com flap a 60°, o coeficiente de sustentação máximo é 1,75 a um ângulo de ataque de 60°. Logo . Substituindo
Com isso, conseguimos calcular a velocidade de aterrissagem. Da relação dada no enunciado:
Convertendo para km/h
Encontramos a velocidade de aterrisagem! o/
Resposta
Exercício Resolvido #7
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 597, ex. 9.137
(Adaptada) Um modelo de aerofólio com corda de 15 cm e envergadura de 60 cm é colocado em um túnel de vento com um escoamento de ar igual a 30 m/s (o ar está a 20°C). O aerofólio está montado sobre uma haste suporte cilíndrica com diâmetro e altura iguais a 2 cm e 25 cm, respectivamente. Os instrumentos na base da haste indicam uma força vertical de 50 N e uma força horizontal de 6 N. Calcule o coeficiente de sustentação do aerofólio.
Dados:
Passo 1
Esse exercício tem bastante informação, mas, quais variáveis precisamos saber para calcular o coeficiente de sustentação ?
Vamos juntos nos lembrar da definição dele:
Precisamos então da força de sustentação , massa específica do fluido , velocidade do fluido V e área projetada.
A força de sustentação atua no eixo y (vertical). Logo, pelo o enunciado:
A velocidade e massa específica foram dadas diretamente. Quanto a área, ela é o comprimento da corda vezes o tamanho da envergadura
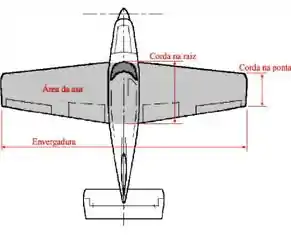
Substituindo na fórmula do coeficiente de sustentação
E assim encontramos o coeficiente de sustentação nesse caso :D
Resposta
Exercício Resolvido #8
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 526, ex. P 7.118
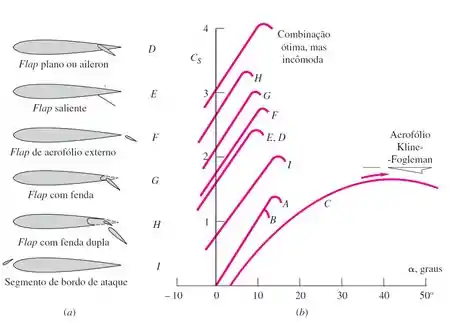
(Adaptada) Admita que um certo avião seja equipado com os melhores dispositivos de alta sustentação da figura abaixo. Qual a sua mínima velocidade de estol em km/h? Este avião pesa 180 kN e tem uma área de asa de 160 m² e uma corda média de 4 m. Sabendo que o avião é projetado para pousar a , qual é a velocidade de aterrissagem apropriada em km/h?
Dados:
Passo 1
E aí! Vamos começar calculando a velocidade de estol. A fórmula dela é
Conhecemos o peso e a área projetada e massa específica do ar. O gráfico dado no enunciado vai ajudar a gente a encontrar o coeficiente de sustentação máximo. Mas qual seria esse valor?
Vamos ter em mente que no enunciado não foi dito qual o tipo do aerofólio (se é flap saliente, flap com fenda, etc..). Mas foi dito que é o disposivo de mais alta sustentação. Ou seja, é aquele com maior no gráfico. Logo

Pelo gráfico,
Substituindo para encontrar velocidade de estol
Passo 2
Agora é possível calcular a velocidade de aterrissagem. No enunciado foi dito que
Finalmente, vamos converter para km/h
Essa é a velocidade de aterrisagem!