Condições de Contorno
Produzido por Raphael EloiTeoria
Quando estamos resolvendo problemas de transferência de massa, eventualmente a gente esbarra com aquelas famosas EDO’s e EDP’s pra resolver. E pra isso a gente precisa de condições de início ou condições de contorno.
Mas relaaaxa, você vai ver agora como e quando usar cada uma delas!
Problemas Transientes
Quando seu problema se passa ao longo do tempo, ou seja,ou você quer descobrir o tempo que passou ou qual é a concentração depois de um tempo , uma das condições que pode ser usada é a condição de início. Ela tem essa cara aqui:
Em outras palavras, quando o tempo é igual à zero, a concentração é igual à concentração inicial.
Condição de Contorno Espaciais
Não precisa ser astronauta pra resolver isso aqui não. Vamos ver agora as condições de contorno relativas ao espaço físico em que o problema está acontecendo!
- Valor Especificado na Superfície:
- Fluxo Especificado na Superfície:
- Convecção na Superfície:
- Reação Química na Superfície:
Quando uma superfície se encontra saturada, significa que ela não tem mais como receber mais nada, assim ela está na condição de doar massa daquela espécie.
Além de todas essas formas de representar a condição de uma superfície, quando falamos de gases, também é possível representar a concentração em termos da pressão parcial usando a Lei de Dalton:
Onde é a pressão total do sistema.
Quando a difusão acontece de uma fase líquida para uma fase gasosa, a gente usa a Lei de Raouult, pra solução líquida ideal:
Onde é a pressão de vapor da espécie A.
Podemos ter um fluxo de massa constante na superfície.
Um caso específico de fluxo constante é quando a superfície é impermeável. Ai nesse caso não tem fluxo na superfície!
Pensa, por exemplo, num copo com água e uma pastilha no fundo. Os componentes da pastilha se transportam pelo copo através de difusão. Agora imagina que na sala onde está esse copo tem um ventilador ligado. Quando a superfície do copo chega a uma condição de saturação, como a gente falou lá em cima, não tem mais como essa superfície receber mais massa desses componentes, nessa hora os componentes são perdidos pela convecção do ar que está em movimento em contato coma superfície desse copo.
Nesse caso, a condição limite da superfície é a de convecção, e ela vai ter essa carinha aqui:
Onde é o coeficiente de convecção mássica e é a concentração na corrente de fluido exerno.
Obs.: A convecção mássica é muito parecida com a convecção térmica, só muda é que ao invés de usarmos os termos relacionados à temperatura, usamos para concentração.
Se a superfície for um catalisador, um metal sofrendo corrosão, ou qualquer outra situação onde as moléculas aparecem ou desaparecem na superfície de acordo com uma reação química.
Onde é a constante da taxa de reação de 1ª ordem.
Os fluxos molares das espécies se relacionam pela estequiometria. Por exemplo:
Se a reação for muito rápida e for reagente, a gente pode considerar .
Esses são os principais casos que vamos ver na transferência de massa, bora então praticar!
Problemas Transientes
Condição de Contorno Espaciais
Exercícios Resolvidos
Exercício Resolvido #1
Transferência de calor e massa - 4ª Edição - Çengel e Ghajar
Gás hélio está armazenado a em um vaso esférico feito com sílica fundida (), que tem um diâmetro de e uma espessura de parede de . Se o vaso é carregado até uma pressão inicial de , qual é a taxa na qual essa pressão diminui com o tempo?
Dados para Hélio-Sílica fundida a : e .
Passo 1
Fala aí! Vamos começar anotando nossos dados! Temos uma parede com:
E um vaso esférico com:
Ela está entre dois meios que tem hidrogênio, e cada lado possui:
O enunciado quer a taxa em que a pressão vai diminuir com o tempo , ok?
Antes de ir para a diversão dos cálculos, vamos fazer algumas considerações importantes para nos facilitar, beleza?
Como o diâmetro é muito maior que a espessura vamos considerar que estamos trabalhando com uma parede plana, com difusão em uma única direção. Além disso, vamos considerar um regime estacionário, com o hélio se comportando como gás ideal e que a pressão do hélio no ar exterior será desprezível… Isso vai nos ajudar bastante!
Passo 2
Vamos lembrar que, pela conservação das espécies:
E que, por causa da difusão através da sílica:
E o acúmulo de massa é dado por:
Opa! Então nosso balanço será:
Sendo e usando a lei dos gases ideais, podemos ter que:
Então:
Opa! Substituindo isso em nosso balanço, teremos:
Reorganizando para ficar apenas com a taxa de pressão com o tempo, vamos ficar com:
Passo 3
Chegou a hora de lembrar da lei de Fick, para ter a seguinte relação:
Isso quer dizer, nas nossas condições, que:
Para achar e vamos usar a massa molar e a solubilidade, olha só:
Agora substituindo isso na nossa relação ali de cima, temos:
Agora a gente pode substituir isso aí lá no nosso balanço e ficar com:
Passo 4
Sendo a área e o volume, dados por:
Nosso balanço vai ficar:
Arrumando isso aí e cortando quem a gente pode, vamos ter:
Usando como constante dos gases , e substituindo os nossos dados, temos:
Logo, a taxa de variação da pressão será:
Show de bola! Terminamos!
Resposta
Exercício Resolvido #2
USP - Transferência de massa - Aula 01
Calcular os dados de equilíbrio sob a forma versus para o sistema m-xileno / o-xileno à pressão total de ( e são as frações molares de m-xileno na fase líquida e na fase vapor respectivamente). São dadas as pressões de vapor dos componentes em atm na tabela a seguir:
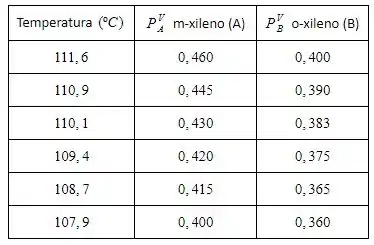
Passo 1
Bom, vamos começar lembrando da nossa teoria e anotando o seguinte:
Para o m-xileno:
Para o o-xileno:
Opa! Então a gente tem que:
E se a gente somar essa relação com a do m-xileno, teremos:
Então nosso será:
E sendo assim, o nosso tem que ser:
Olha só que show! Já podemos encontrar o e o , para cada caso da nossa tabela, né?
Mas e as frações de B? Relaxa! Agora vai ser de boa! A soma das frações tem que ser , certo? Então, temos que:
Show de bola! Achando um encontramos o outro!
Passo 2
Agora é a hora das continhas, vamos fazer primeiro para o A, ok?
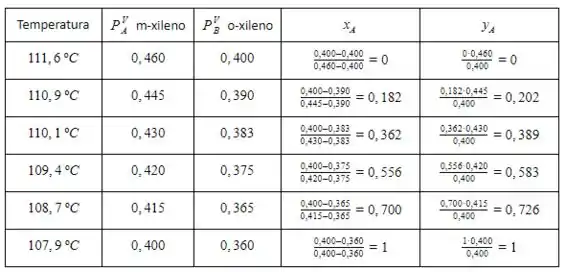
Agora vamos fazer as continhas para o B:
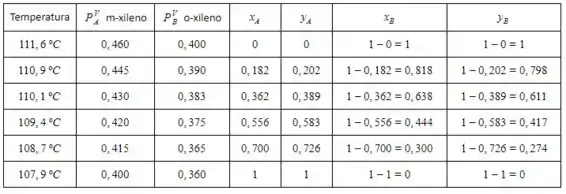
Show de bola!
Resposta
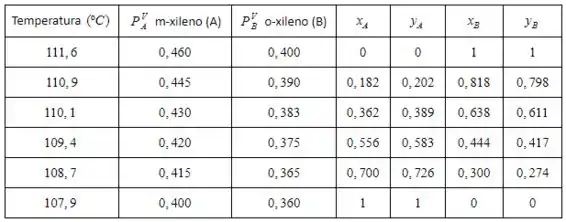
Exercício Resolvido #3
Universidade Federal de São Carlos - Balanço de massa na análise de processos químicos
Dez metros cúbicos de uma solução de cloreto de sódio são misturados com de uma solução de sulfato de amônio . Supondo constantes e iguais as massas específicas das duas soluções e da solução resultante, obtenha as concentrações em dos íons cloreto () e amônio () na solução resultante.
Passo 1
Pelo balanço de massa, nosso velho conhecido, sabemos que:
Tranquilo? Bom, nós temos uma solução de , que vamos chamar de solução , temos uma solução de , que vamos chamar de solução , e temos a solução que resulta da mistura, que vamos chamar de solução , certo?
Então, nós temos o seguinte:
E lembrando que , temos:
Mas o enunciado pediu pra gente considerar que as massas específicas são iguais , logo:
E os volumes de e de foram dados, então:
Passo 2
A gente pode supor que os sais estão se dissociando totalmente, então teremos o seguinte:
Opa! Sabemos o volume das soluções, então podemos fazer o seguinte para encontrar as concentrações, primeiro para o :
Lembrando que a concentração foi pedida em vamos converter o valor que o enunciado nos deu usando a massa molar do , olha só:
E convertendo o volume para litro, teremos:
Substituindo tudo isso, vamos ter uma concentração de ,na solução:
Teremos então:
Agora vamos fazer a mesma coisa para o :
Fazendo a mesma conversão, agora usando a massa molar do , temos:
Convertendo o volume para litro, teremos:
Substituindo tudo temos:
Teremos então uma concentração de de:
Prontinho!
Resposta
Exercício Resolvido #4
Universidade Federal de São Carlos - Balanço de massa na análise de processos químicos
No processo de fabricação de etanol, o mosto de fermentação é preparado a partir da diluição de melaço (mel final) com água ou com caldo de cana. As massas específicas e as concentrações em grau Brix desses fluidos são apresentadas na tabela a seguir. Grau Brix representa a porcentagem em massa de sólidos solúveis contida em soluções aquosas de açúcares ou fração mássica (). É uma medida indireta do teor de açúcares em soluções, uma vez que a maioria dos sólidos solúveis nesses fluidos são açúcares.
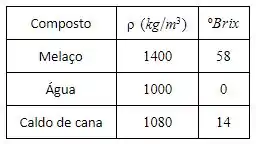
Supondo que a vazão de mosto que alimenta uma dorna de fermentação seja de e que o mesmo deva ter uma concentração de . Calcular as vazões de melaço e de água e de melaço e de caldo de cana, dependo do tipo da diluição (com água ou caldo) e as respectivas massas específicas dos mostos , supondo que a massa específica da mistura seja dada por:
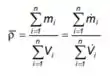
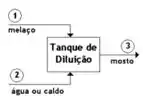
O fluxograma do processo de diluição com água ou caldo de cana (corrente 2) é ilustrado na Figura:
Passo 1
Fala aí! Olha esse enunciado cheio de informação…

Relaxa! O que ele quer é que a gente encontre as vazões de melaço-água e melaço-cana, vamos nessa então!
Bom estamos trabalhando com um processo contínuo e estacionário, né? Pelo balanço de massa a gente vai ter que:
Sendo assim, temos que:
E lembrando que :
Beleza? Agora vamos pensar primeiro na diluição da água:
Humm… Não temos as duas vazões e nem o , mas e se a gente fizer o balanço para os sólidos? Vamos ver se encontramos alguma coisinha que nos ajude!
Vamos ter então:
Substituindo nossos dados, teremos:
Opa! Então descobrimos que:
Agora substituindo o lá na outra equação, vamos ter:
Daí nós conseguimos tirar uma relação de com , ficando com:
Passo 2
Lembrando que:
Substituindo os valores que temos nessa relação, podemos encontrar o :
Show! Agora podemos encontrar o e o , olha só:
Então o , será:
Agora vamos repetir o mesmo procedimento para a diluição do caldo de cana, beleza?
Passo 3
Para o caldo teremos:
Fazendo o balanço para os sólidos, temos:
Então:
Substituindo nossos dados:
Logo:
Agora substituindo o na equação, vamos ter:
Nossa relação de com agora fica:
E sendo assim o nosso , pode ser escrito como:
Passo 4
Usando a relação onde:
Podemos substituir o que descobrimos e teremos:
Sendo assim, vamos ter agora que e o , serão:
Agora o :
Uhul! Arrasamos!
Resposta
Para a água: e ;
Para o caldo de cana: e .
Exercício Resolvido #5
Universidade Federal de São Carlos - Balanço de massa na análise de processos químicos
O fluxograma do processo de recuperação de um produto farmacêutico é apresentado na Figura. Trata-se de um processo com múltiplas unidades, com reciclo e sem reação química no estado estacionário.
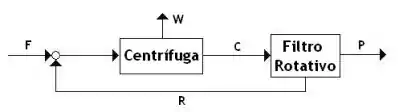
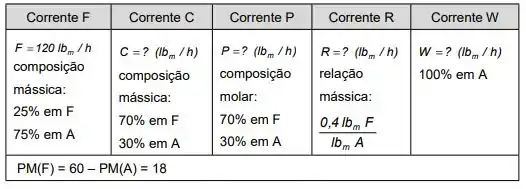
Denominado o produto farmacêutico como F e a água como A, calcule os valores das variáveis indicadas na Tabela que segue.
Passo 1
Bora pra mais uma? Partiu! Bom, esse enunciado quer que a gente resolva todos os itens que estão faltando nessa tabela… Vamos lá!
Pra começar vamos encontrar a composição mássica de P, beleza?
Agora vamos usar a relação:
Opa! Vamos ter então que:
E teremos também:
Passo 2
Agora é a vez da composição mássica de R! A tabela nos dá a relação:
Isso quer dizer que:
Logo:
E a gente sabe que , então podemos encontrar as frações fazendo assim:
Teremos então:
Agora que a gente tem as frações molares, podemos partir para o balanço de massa!
Passo 3
Vamos começar nosso balanço, usando o primeiro volume de controle, que compreende o processo como um todo, ok? Vamos ter que:
Agora fazendo o balanço para o F, teremos:
Daqui tiramos:
E substituindo na equação lá de cima, vamos ter:
Opa! Estamos quase lá! Agora vamos usar o volume de controle que envolve o filtro radioativo (correntes C, P e R)... Temos então:
E substituindo , ficamos com:
Agora se a gente fizer um balanço para , teremos:
Substituindo a galera toda, vamos ficar com:
Bom, agora se a gente substituir o , temos:
E agora podemos encontrar o :
Prontinho! Encontramos tudo que estava faltando!
Resposta
Exercício Resolvido #6
Universidade Federal de São Carlos - Balanço de massa na análise de processos químicos
O bagaço de cana, que representa da cana-de-açúcar em massa, apresenta a seguinte composição mássica típica: de água, de carbono, de oxigênio e de hidrogênio. Supondo que da combustão do bagaço seja parcial ou incompleta e considerando que do bagaço produzido seja queimado na caldeira para geração de vapor numa usina, calcular por tonelada de cana moída:
- as quantidades de e de produzidas.
- a quantidade alimentada de ar supondo um excesso de .
Passo 1
Olha só, temos duas letrinhas para resolver! Vamos começar pela letra a! Ela quer as quantidades de e de que foram produzidas no processo.
Pra achar, vamos começar calculando a quantidade de bagaço de cana queimada… Primeiro temos que lembrar que se temos:
E o enunciado disse que o bagaço da cana representa da cana-de-açúcar em massa, isso quer dizer:
Então vemos que:
Logo, nossa quantidade de bagaço de cana por tonelada é:
Essa vai ser a nossa base de cálculo, beleza?
Se está acontecendo uma combustão, então nós estamos trabalhando com reação química, certo? Então vamos converter a quantidade e a composição mássica em grandezas molares!
Para isso vamos usar as relações:
e
Dando uma relembrada nas massas molares, temos:
Opa! Então isso quer dizer que:
E sendo a quantidade correspondente a , em mols, é:
Passo 2
Então a composição molar do bagaço será:
E sendo assim agora a gente só precisa lembrar das reações de combustão e encontrar as quantidades pedidas, olha só:
Show! A quantidade de , será dada por:
E a quantidade de , será:
Finalizamos a letra a!
Passo 3
Vamos agora para a letra b! Precisamos das quantidades de oxigênio teórico e alimentado, certo? Vamos achar usando a relação:
Teremos então:
Agora fazendo o mesmo para o oxigênio alimentado, temos:
Substituindo o valor que encontramos para o oxigênio teórico:
Ficaremos com:
E pra fechar vamos encontrar a quantidade de ar alimentado:
Substituindo o valor que encontramos:
Conseguimos!
Resposta
- e ;
- .
Exercício Resolvido #7
Universidade Federal de São Carlos - Balanço de massa na análise de processos químicos
No processo Haber-Bosch de produção de amônia, o hidrogênio ( ) proveniente de gás natural e o nitrogênio () proveniente do ar reagem em condições elevadas de pressão e temperatura ( e ), de acordo com a seguinte equação:
Os reagentes são alimentados no processo na razão molar de , e a conversão global em relação ao hidrogênio () é de . Considerando que a unidade de separação recicla dos reagentes não convertidos no reator, calcule a conversão no reator e a taxa de reciclo numa planta que produz por dia.
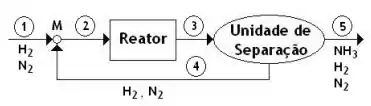
Pode-se notar que se trata de um processo contínuo com reciclo e com reação no estado estacionário. O fluxograma da Figura ilustra o processo em questão.
Passo 1
Fala aí! Vamos resolver mais uma questãozinha! Bom, o enunciado quer que a gente calcule a conversão no reator e a taxa de reciclo, nas condições dadas, então vamos dar isso a ele!
Pra começar ele disse que a razão molar se comporta assim:
E que nossa planta produz / dia, isso quer dizer qu:
Para fazer a conversão global para o , podemos usar a relação:
Então temos que:
E o enunciado falou que a unidade recicla dos reagentes e saem na corrente 5, então:
e
Passo 2
Fazendo o balanço para o hidrogênio, vamos ter que:
O caminho que o hidrogênio percorre é: entrando na corrente 1 e saindo na corrente 5, logo vamos ter:
E isso nos diz que:
Substituindo isso aí na equação da conversão global do passo 1, temos:
E teremos:
E pela relação dada pelo enunciado, vamos ter:
E com esses resultados nós podemos voltar lá nas equações do passo 1 e achar:
E também podemos encontrar:
Passo 3
Agora se a gente fizer um balanço para o no ponto M, vamos ter que:
Substituindo teremos:
Sendo assim, com esses dados, podemos achar a conversão no reator:
ou
E a taxa de reciclo será dada por:
Uhul!! Conseguimos!
Resposta
Exercício Resolvido #8
Universidade Federal de São Carlos - Balanço de massa na análise de processos químicos
Uma das etapas do processo de produção de açúcar é a clarificação do caldo com a queima de enxofre produzindo que em contato com a água presente no caldo, gera e abaixa o pH do caldo, precipitando e flotando impurezas presentes no caldo de cana. Trata-se de um processo contínuo com reação no estado estacionário. A reação global é dada por:
Considere o fluxograma de sulfitação da Figura:
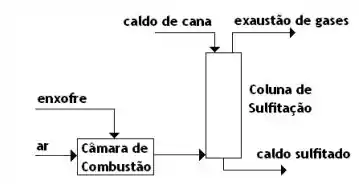
Se uma unidade de sulfitação processar de caldo de cana reduzindo o pH do caldo de para ; calcule as vazões de alimentação requeridas de enxofre (em ) e de ar (em a e ), supondo que o mesmo esteja em excesso de .
Passo 1
Vamos arrasar em mais uma questão! Bom, o enunciado deu pra gente os valores de pH na entrada e na saída, isso nos permite saber a concentração de nesses dois momentos, então vamos achar:
Logo, nós teremos que:
e
Fazendo o balanço de massa, sem esquecer que temos geração também, teremos:
Isso significa que:
Se a gente supor que as massas específicas são iguais, temos , aí poderemos fazer a relação:
Passo 2
Lembrando que ácidos fortes, tendem a ionização total, vamos então considerar que isso está acontecendo com o ácido sulfúrico:
Vamos então calcular a quantidade de que foi gerada:
Observando a estequiometria da reação dada, temos que:
Opa! Então quer dizer que:
Show! Agora vamos fazer o balanço de massa para o enxofre! Pra começar vamos supor que todo enxofre que é alimentado é consumido, beleza? Então:
Opa! Então:
Logo, temos que:
Passo 3
Agora partiu calcular a quantidade de ar alimentado, para isso precisamos da quantidade de , vamos achá-lo!
E como:
Teremos uma quantidade de ar alimentado, como sendo:
Passo 4
Mas o enunciado pediu pra gente a quantidade de ar alimentado, em e estando a e … Para isso, vamos considerar o ar como um gás ideal, e usando a constante dos gases como sendo , temos:
Substituindo nossos valores, temos:
Show de bola! Conseguimos!