Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 144
12-144 Ar entra em um duto adiabático de 4 cm de diâmetro a condições de entrada de , e , e sai a um número de Mach de . Assumindo o fator médio de atrito de 0,03, determine velocidade, temperatura e pressão na saída do duto.
Passo 1
Vamos lá!! Temos aqui um escoamento de Fanno e queremos e ! O enunciado da pra a gente os dados de e isso quer dizer que podemos usar as relações da tabela pra encontrar o que queremos!
Aqui temos um esqueminha do que ta acontecendo e para vizualizar melhor o problema:
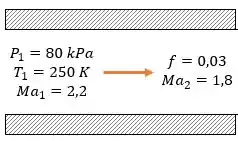
Vamos então já reunir todos os dados da tabela :
Passo 2
Conhecemos , então vamos começar por aqui:
Lembrando que
Passo 3
Agora , seguinto o mesmo raciocínio:
Se :
Passo 4
Por fim :
Então:
Mas não conhecemos !
Podemos fazer:
Onde :
Lembrando que e
E :
Podemos finalmente achar :
Resposta
Exercícios de Livros Relacionados
Hélio entra em um bocal a 0,8 MPa, 500 K e a uma velocidade de 120 m/s. Considerando o escoamento isentrópico, determine a pressão e a temperatura do hélio em um local onde avelocidade do ar é igual à
Para o canal do problema FE10.1, se Q = 24 m3/s e a profundidade é 2 m, qual é o número de Froude do escoamento?(a) 0,50, (b) 0,77, (c) 0,90, (d ) 1,00, (e) 1,11m
Se o canal do problema FE 10.1 for construído em pedra argamassada (fator de Manning n = 0,020), qual é a vazão de escoamento uniforme quando a profundidade da água é de 2 m? (a) 6 m3/s, (b) 18 m3/s,
Para o canal do Problema FE10.1, se o coeficiente de rugosidade de Manning é n = 0,020 e Q = 29 m3/s, qual é a profundidade normal yn? (a) 1 m, (b) 1,5 m, (c) 2 m, (d) 2,5 m, (e) 3 m
Para o canal do problema FE10.1, se Q = 24 m3/s, qual é a profundidade crítica yc?(a) 1,0 m, (b) 1,26 m, (c) 1,5 m, (d) 1,87 m, (e) 2,0 m