Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 94
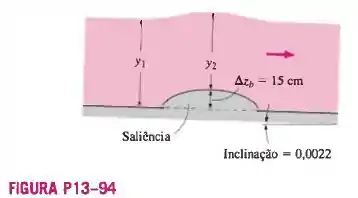
13-94 Considere o escoamento uniforme da água em um canal largo feito de concreto não polido assentado sobre uma inclinação de 0,0022. Agora a água escoa sobre uma saliência com
15 cm de altura. Se o escoamento sobre a saliência for exatamente crítico (Fr =1), determine a vazão e a profundidade de escoamento sobre a saliência por m de largura.
Passo 1
Pronto pra mais uma questão?!!
Vamos lá, a gente quer encontrar a vazão volumétrica do escoamento e a profundidade !! Não temos tantos dados como gostariamos mas vamos seguir em frente!
Primeiro a vazão:
Não conhecemos a largura do canal , então vamos assumir . O raio hidráulico e e lembrando que , para o concreto não polido , substituindo:
Arrumando:
Outra forma de calcular a vazão é usando a velocidade:
Sabendo que e considerando :
Esse pode ser ou .
Não conhecemos a velocidade também! A nossa tática vai ser usar todas as equações que tivermos disponível para achar a vazão e a profundidade !!
Passo 2
O problema diz que em cima da saliência o escoamento é crítico, então:
Para :
Arrumando:
Podemos calcular também:
Sabedo que :
Ficamos com:
Passo 3
e são funções de , então podemos usar a seguinte relação para finalmente achar :
Substituindo:
Essa equação não parece nada fácil de resolver, heim!? Mas relaxa que vamos usar o solver do excel!
Escrevemos as duas equações, chutamos um , aqui eu chutei e pedimos pra o excel dizer pra a gente o valor para para que os dois lados da equação sejam iguais:
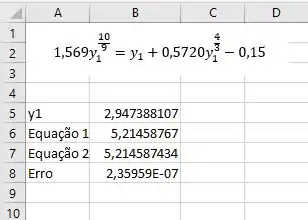
Achamos aproximadamente.
Passo 4
Agora podemos substituir aqui:
Calculando:
E :
Calculando achamos: