Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 109
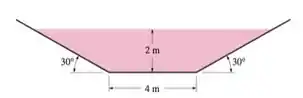
Um canal trapezoidal com revestimento de tijolos tem uma inclinação do fundo de 0,001 e uma largura de base de 4 m, e as superfícies laterais tem ângulos de 30˚ da horizontal, como mostra a figura. Se a profundidade normal for medida como 2 m, estime a vazão de água através do canal.
Passo 1
Fala ai! Pra resolver essa questão primeiro vamos ter que assumir algumas coisas: o escoamento é permanente e uniforme, a inclinação do fundo é constante e a rugosidade do canal também é constante.
A vazão de escoamento é dada pela equação de Manning:
A inclinação do fundo o problema já deu:
Além disso, na tabela 13-1 temos que o coeficiente de Manning pra um canal de tijolo:
E a gente também vai precisar saber calcular algumas coisas.
A área transversal do canal:
Onde b é a largura da base e h é a altura do nível (profundidade).
O perímetro “molhado”:
E o raio hidráulico:
Então bora começar a fazer conta!
Passo 2
Vamos começar então calculando o que a gente precisa saber pra calcular a vazão:
Agora podemos calcular o raio hidráulico:
Passo 3
Agora que temos tudo, finalmente podemos calcular a vazão!