18. Considere o escoamento de ar sobre uma placa plana com comprimento L = 1m, sob condições nas quais a transição ocorre em xc = 0,5 m baseada em um número de Reynolds crítico de Rex,c = 5 × 105.

(a) Calculando as propriedades termofísicas do ar a 350 K, determine a velocidade do ar.

(b) Nas regiões laminar e turbulenta, os coeficientes convectivos locais são, respectivamente, hlam(x) = Clamx−0,5 e hturb(x) = Cturbx−0,2 nas quais, em T = 350 K, Clam = 8,845 W/(m3/2 · K), Cturb = 49,75 W/(m1,8· K) e x possui unidade de m. Desenvolva uma expressão para o coeficiente convectivo médio, hlam (x), como uma função da distância da aresta frontal, x, para a região laminar, 0 ≤ x ≤ xc.

(c) Desenvolva uma expressão para o coeficiente convectivo médio, turb (x), como uma função da distância da aresta frontal, x, para a região turbulenta, xc ≤ x ≤ L.

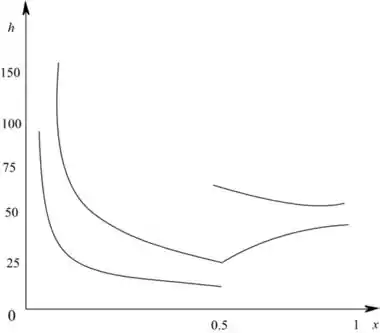
(d) Nas mesmas coordenadas, represente os coeficientes convectivos locais e médios, hx e x, respectivamente, em função de x para 0 ≤ x ≤ L.

Letra (b)

Escreva a expressão para o coeficiente de convecção médio para fluxo laminar da seguinte maneira:

Distância da borda principal,  para a região laminar,

Substitua por .

Substituto .

Portanto, o coeficiente de convecção médio para a região laminar é 

Letra (c)

Escreva a expressão para o coeficiente de convecção médio da região turbulenta da seguinte forma:

Distância da borda principal,  x c ≤ x ≤ L

Reescreva a Equação (1) como,

Substitua na Equação (2).

Portanto, a convecção média na região turbulenta é.

Letra (d)

Desenhe o gráfico entre os coeficientes local e médio no intervalo,  como na Figura (2).