Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 26
Considere uma aleta retangular que é usada para resfriar o motor de uma motocicleta. A aleta possui 0,15 m de comprimento e está a uma temperatura de 250 °C, quando a motocicleta se desloca a uma velocidade de 80 km/h em ar a 27 °C. O ar encontra-se em escoamento paralelo às superfícies da aleta e condições de escoamento turbulento podem ser admitidas ao longo de toda a superfície.
- Qual é a taxa de remoção de calor por unidade de largura da aleta?
- Gere um gráfico da taxa de remoção de calor por unidade de largura da aleta para velocidades da motocicleta entre 10 e 100 km/h
Passo 1
É sempre importante começarmos estas questões com as nossas hipóteses para o problema. Neste caso, temos escoamento em regime permanente, propriedades constantes do ar e consideraremos escoamento turbulento (imposição da questão).
Nosso primeiro passo é determinar a taxa de transferência de calor por unidade de largura saindo da aleta. Temos que tomar muito cuidado para não esquecer as duas superfícies da aleta no cálculo da taxa (representada pelo número 2). Sendo assim, esta taxa será dada por:
Então, o trabalho deste item será determinar o coeficiente médio de transferência de calor.
Mas, antes disto, vamos aproveitar para obter as propriedades do ar. Consideraremos que o ar está a 1 atm e a temperatura do filme é .
Utilizando a tabela , temos: , , . Detalhe que obtivemos todos os dados a partir da interpolação da tabela.
Passo 2
Agora, vamos calcular o coeficiente de transferência de calor. Para isto, precisamos saber qual a correlação correta para o número de Nusselt médio. Como a placa está sob escoamento turbulento, a correlação correta é:
Calculando o número de Reynolds, temos:
Portanto, o coeficiente de transferência de calor médio é:
Portanto, a taxa de transferência de calor por unidade de largura é:
Passo 3
Para finalizarmos a questão, precisamos obter um gráfico que relaciona a velocidade de saída da moto com a taxa de transferência de calor por unidade de largura da aleta.
E, na grande realidade, esta pergunta é bem simples. Podemos afirmar isto pois nós já temos a função para plotar.
Basta voltar no Passo anterior e, ao invés de substituir o número de Reynolds como um número, é só colocar ele como função de . Portanto,
Agora, se substuirmos os valores de todas as constantes do problema, com exceção de , temos:
Analisando a função acima, o termo de velocidade está em . Para podermos plotar a função em , basta fazer uma pequena correção, a qual é:
Agora sim, plotando a função acima, temos:
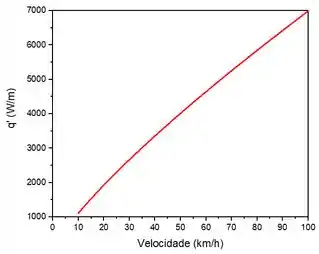
Resposta
