Gás hélio a uma temperatura de corrente livre de está em fluxo paralelo sobre uma placa plana de comprimento e temperatura . Entretanto, os obstáculos colocados no fluxo intensificam o escoamento com o aumento da distância em relação à aresta frontal, a variação espacial das temperaturas medida na camada limite é correlacionada por uma expressão da forma , onde e estão em metros. Determine e plote a maneira na qual o coeficiente de convecção local varia com . Avalie o coeficiente de convecção médio para a placa.
Passo 1
Beleza, a gente tem a equação que descreve a temperatura em função do comprimento da barra e da altura da massa de gás que está escoando. A questão pede para encontrarmos o coeficiente convectivo local que é dado pela equação:
Passo 2
Vamos então primeiro calcular a derivada da função de temperatura em relação a :
E aplicamos o ponto :
Depois colocamos esse resultado na função :
Passo 3
Para determinarmos o que é a condutividade térmica do hélio, precisamos fazer a média entre o valor de temperatura da placa e o valor de temperatura da corrente livre:
Esse valor corresponde a aproximadamente
Substituindo ele junto com e :
Passo 4
Como dá para ver, cresce linearmente com com um coeficiente muito alto para o comprimento da placa que é só , o gráfico é praticamente uma reta vertical:
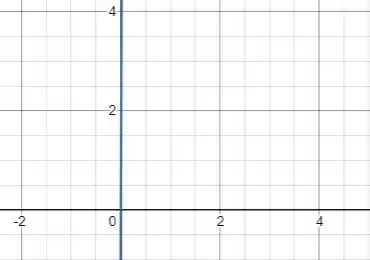
Passo 5
Para calcularmos o coeficiente convectivo médio, , basta integrarmos a função de a e depois dividirmos pelo comprimento da placa, assim:
Ou seja, como se trata de uma função, é necessário somar todos os valores dela no intervalo em que ela está definida (o comprimento da placa) e depois dividir por esse intervalo.