Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 183

183 – Uma típica seção da parede de um edifício é mostrada na Fig. P3-183. Essa seção estende-se para dentro e fora da folha e é repetida no sentido vertical. Os suportes de apoio da parede são feitos de aço k = 50 W m ⋅ K e mede 8   c m   ( t 23 ) × 0,5   c m   ( L g ) . O restante do espaço interno da parede é preenchido com isolante k = 0,03 W m ⋅ K medindo 8   c m   ( t 23 ) × 60   c m   ( L a ) . A parede interna é de placas de gesso k = 0,5 W m ⋅ K de 1   c m de espessura t 12 , e a parede externa é de tijolos k = 1,0 W m ⋅ K de 10   c m de espessura ( t 34 ) . Qual é a temperatura da superfície interna do tijolo, (3) quanto T 1 = 20   ℃ e T 4 = 35   ℃ ?

Passo 1

Para facilitar, desenhe o esquema descrito no problema.

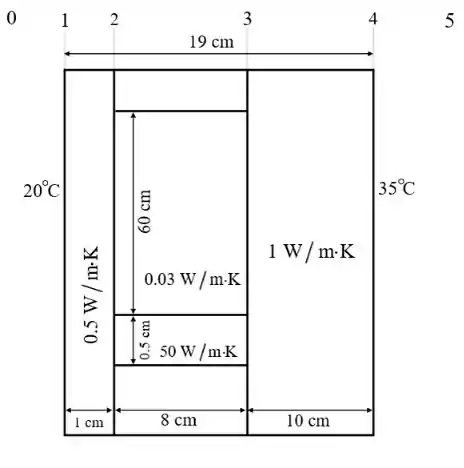
Passo 2

Considere o seguinte circuito térmico para o diagrama referente a Fig, P3-183.

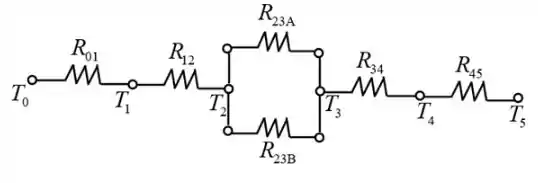
Passo 3

Vamos calcular a resistência condutiva térmica do gesso.

R 12 = t 12 k g e s s o

= 0,01 0,5

R 12 = 0,02 m 2 ⋅ ℃ W

Vamos calcular a resistência condutora do isolante.

R 23 A = t 23 L A k i s o l a n t e L A + L B

= 0,08 × 0,6 0,03 × ( 0,6 + 0,05 )

R 23 A = 2,645 m 2 ⋅ ℃ W

Vamos calcular a resistência condutora do aço.

R 23 B = t 23 L B k a ç o L A + L B

= 0,08 × 0,005 50 × ( 0,6 + 0,05 )

R 23 B = 1,32 × 10 - 5   m 2 ⋅ ℃ W

Vamos calcular a resistência condutora do tijolo.

R 34 = t 23 k t i j o l o

= 0,01 1 0

R 34 = 0,1     m 2 ⋅ ℃ W

Passo 4

Vamos calcular a resistência condutora térmica total.

R t o t a l = R 12 + 1 1 R 23 A + 1 R 23 B + R 34

R = 0,02 + 1 1 2,645 + 1 1,32 × 10 - 5 + 0,1

R t o t a l = 0,12 m 2 ⋅ ℃ W

Calcule a taxa de transferência de calor constante, que será a mesma em toda a parede.

q = T 4 - T 1 R

= 35 - 20 0,12

= 125 W m 2

Passo 5

Calcule a temperatura na superfície do tijolo interno, isto é, superfície  3 .

R 34 = T 4 - T 3 q

0,1 = 35 - T 3 125

T 3 = 22,5   ℃

Portanto, a temperatura na superfície do tijolo interno será  22,5   ℃ .

Resposta

Portanto, a temperatura na superfície do tijolo interno será  22,5   ℃ .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma parede de 4,5 m de comprimento, 3,0 m de altura e 0,22 m de espessura de concreto ( k = 1 , 1W / m ⋅ K ) . As temperaturas do projeto do ar interno e externo são 24 °C e 3 °C, respectiva
Aproximadamente 10 6 componentes elétricos discretos podem ser colocados em um único circuito integrado (chip), com uma dissipação térmica na ordem de 30.000W / m 2 . O chip, que é muito fino, tem a s
Um sistema térmico específico envolve três objetos de forma fixa com resistências condutivas R 1 = 1 K / W ,R 2 = 2K / W e R 3 = 4K / W , respectivamente. Um objetivo é minimizar a resistência térmica
O desempenho de motores de turbina a gás pode ser melhorado pelo aumento da tolerância das pás da turbina aos gases quentes que emergem do combustor. Um procedimento que permite atingir altas temperat
Considere uma parede plana composta constituída por dois materiais com condutividades térmicas k A = 0,1W / ( m · K ) e k B = 0,04W / ( m · K ) e espessuras L A = 10m m e L B = 20m m . A resistência d