Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 39
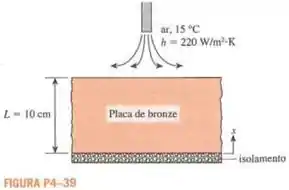
Uma placa de bronze quente está tendo a superfície superior refrigerada por jato de ar a uma temperatura de , e o coeficiente de transferência de calor por convecção é de . A placa de bronze de de espessura, tem temperatura uniforme inicial de , e sua superfície inferior é isolada. Determine a temperatura no centro da placa de bronze após minutos de resfriamento.
Passo 1
Podemos perceber que este é um caso de condução em grandes paredes planas, a dimensão da placa na direção é muito grande. Além disso, um lado da parede é adiabático.
Para determinar a temperatura no centro da placa de bronze após minutos de resfriamento, podemos começar calculando o comprimento da característica.
Com o comprimento característico, podemos calcular o número do Biot usando a seguinte relação:
Aqui, é o coeficiente de transferência de calor por convecção e é a condutividade térmica da placa de bronze. Substituindo por , por e por .
Como o número de Biot não é menor que , a análise de calor em para sistema aglomerado não pode ser aplicada.
Passo 2
Agora, vamos calcular o número de Fourier usando a seguinte relação:
Aqui, é o número de Fourier, é a difusividade térmica do material, é o tempo e é o comprimento crítico da placa. Podemos substituir pelos dados fornecidos, por , por e por .
Passo 3
Agora, vamos usar a equação de distribuição de temperatura para a parede plana usando a aproximação de um termo para calcular a temperatura. A equação é escrita da seguinte maneira:
Aqui é a temperatura do fluido, é a temperatura inicial e é o local. Podemos obter os valores das constantes e usando o número de Biot na tabela 4-2, (Coeficientes utilizados na solução aproximada do termo de condução de calor transiente unidimensional em paredes planas) no livro didático. Assim temos que:
Podemos então substituir os dados fornecido e encontrados, por , por , por , por , por e por , na equação acima. Assim tempos:
Portanto, a temperatura no plano central da placa de bronze após 3 minutos de resfriamento é .