Aproximadamente componentes elétricos discretos podem ser colocados em um único circuito integrado (chip), com uma dissipação térmica na ordem de . O chip, que é muito fino, tem a sua superfície externa exposta a um líquido dielétrico com e , e a sua superfície interna está conectada à placa de circuito. A resistência térmica de contato entre o chip e a placa é de , e a espessura e a condutividade térmica da placa são e respectivamente. A outra superfície da placa está exposta ao ar ambiente, no qual e .
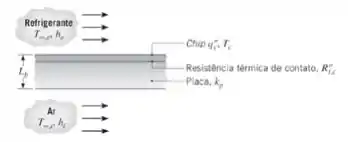
(a) Esboce o circuito térmico equivalente correspondente às condições de regime estacionário. Usando as variáveis, identifique as resistências apropriadas, as temperaturas e os fluxos térmicos.
(b) Sob condições de regime estacionário, nas quais um fluxo térmico dissipado no chip é de , qual é a temperatura do chip?
(c) O fluxo térmico máximo permitido, , é determinado pela restrição de que a temperatura do chip não deve exceder . Determine m para as condições anteriores. Se ar for utilizado no lugar do líquido dielétrico, o coeficiente convectivo é reduzido em aproximadamente uma ordem de grandeza. Qual é o valor de m para Utilizando resfriamento com ar, é possível obter melhorias significativas usando-se uma placa de circuito de óxido de alumínio e/ou empregando-se uma pasta condutiva na interface chip-placa, para a qual ?
Passo 1
Beleza galerinha, vamos lá! Temos que achar o (a) Circuito térmico equivalente, (b) Temperatura do chip, (c) Máxima dissipação de calor permitida para líquido dieléctrico e ar. Efeito das mudanças na temperatura da placa de circuito e na resistência de contato. Portanto, (a):
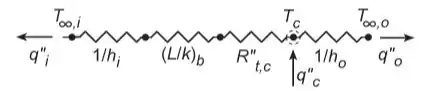
Passo 2
(b) Aplicação de conservação de energia numa superfície de controlo sobre o chip ()
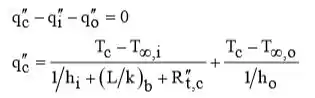
Com , , e ,

Passo 3
(c)Para e , os rendimentos do balanço energético anterior,
![]()
Com e . Substituindo o dielétrico por ar (), os seguintes resultados são obtidos para diferentes combinações de e