37 - Seja o Problema 11.36.
(a) Para , determine as temperaturas de saída do ar e da amônia, assim como a taxa de transferência de calor.
(b) Represente graficamente as temperaturas de saída do ar e da amônia versus a vazão da água no intervalo.
Passo 1
Temos para esse caso a seguinte representação do problema:
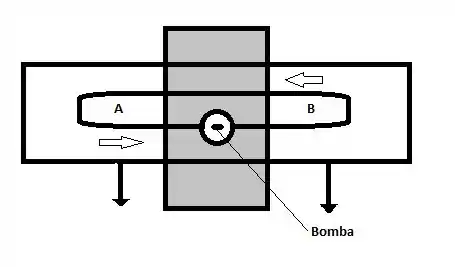
Antes de começarmos o problema, vamos listar alguns dados importantes que nos ajudarão na resolução do problema.
Para o trocador de calor A:
Vazão mássica do ar,
Temperatura de entrada do ar,
Para o trocador de calor B:
Vazão mássica de amoníaco,
Temperatura de entrada de amônia,
Temos também que a vazão mássica da água é igual entre os trocadores,
O produto do coeficiente geral de transferência de calor e da área de transferência de calor é dado por,
Onde,
E
Passo 2
Como as temperaturas de saída dos fluidos não são conhecidas, a temperatura média do fluido não pode ser calculada. Repare que as temperaturas, foram aproximadas e a da água foi uma média.
Para prosseguir, precisaremos obter alguns valores tabelados. Para a água iremos utilizar a tabela A-6, para o ar a tabela A-4 e para a amônia a tabela A-4 também.
Para o ar a uma temperatura de , temos:
Para a amônia a uma temperatura de , temos:
Para a água a uma temperatura de , temos:
Passo 3
a)
Temos A vazão mássica da água no trocador de calor A é igual a vazão no trocador B,
,
Para o trocador de calor A:
Deixei a temperatura de entrada da água como ;
A temperatura de saída da água como ;
e a temperatura de saída do ar como .
O produto do coeficiente geral de transferência de calor e da área de transferência de calor é dado por,
Passo 4
Agora precisamos da taxa de capacidade térmica do ar e da água, que pode ser calculada por meio das seguintes relações:
Para o ar:
Para a água:
Passo 5
Para encontrar a relação da capacidade térmica temos a seguinte relação:
Logo, precisamos encontrar qual é a capacidade máxima e a mínima. Desde então, temos que , assim:
Desse modo:
Passo 6
Temos que o NTU (número de unidades de transferência) é usado para calcular a taxa de transferência térmica em trocadores de calor. Em termos de coeficiente geral de transferência de calor é dado por,
Para o revestimento único, a eficácia do trocador de calor de múltiplas passagens é fornecida por:
Substituindo pelos valores conhecidos, temos:
Passo 7
A taxa de transferência de calor real pode ser determinada de imediato pela expressão 11.22.
Passo 8
Outra expressão que nos ajudar é a 11.18, onde iremos ter mais uma equação em função da transferência de calor tomando o ar como base.
Como queremos saber a temperatura de saída, vamos rearranjar a equação.
Passo 9
Agora temos que repetir todos os passos feitos anteriormente, só que agora para o trocar de calor B.
Trocador de calor B:
Vamos deixar, a temperatura de entrada da água como ;
A Temperatura de saída da água como ;
E a temperatura de saída de amônia sendo .
Dado que a água que sai do trocador de calor A vai para o trocador de calor B e vice-versa,
Isso implica que,
O produto do coeficiente geral de transferência de calor e da área de transferência de calor é dado por,
Passo 10
Agora precisamos da taxa de capacidade térmica da água e da amônia, que podem ser calculadas por meio das seguintes relações:
Para a amônia:
Para a água:
Como .
Desse modo:
NTU em termos de coeficiente geral de transferência de calor é dado por,
Para o revestimento único, a eficácia do trocador de calor de múltiplas passagens é fornecida por:
Substituindo pelos valores conhecidos, temos:
Passo 11
A taxa de transferência de calor real pode ser determinada de imediato pela expressão 11.22.
Outra expressão que nos ajudar é a 11.18, onde iremos ter mais uma equação em função da transferência de calor tomando a amônia como base.
Entretanto, vamos supor que a corrente pega como referência foi a de ar, logo a taxa de transferências da corrente B é negativa pois está cedendo calor para a corrente A (ou se ficar mais fácil para visualizar, imagine que uma corrente está indo de encontro a outra).
Logo:
Como queremos saber a temperatura de saída, vamos rearranjar a equação.
Passo 12
Agora se observar, temos 4 equações:
Entretanto, vamos lembrar que e .
Agora, vamos relembrar que adotamos a temperatura de entrada da água como a temperatura média, logo:
Portanto:
Como estamos trabalhando com um trocador de calor, o calor cedido por um fluido tem que ser o calor ganho pelo outro, já que não temos uma fonte de calor. Desse modo:
Logo:
Passo 13
Agora basta substituirmos esses valores na equação e para obtermos as temperaturas desejadas:
E
Passo 14
b) Precisamos do software IHT.
Resposta
- , e
- É necessário o uso de ferramentas gráficas.