Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 8

Um fluido escoa em regime permanente entre duas placas paralelas. O escoamento é completamente desenvolvido e laminar. A distância entre as placas é h .

(a) Deduza uma equação para a tensão de cisalhamento como uma função de y . Trace um gráfico dessa função.

(b) Para μ = 1,15   N . s / m 2 , ∂ p / ∂ x = 58   P a / m e h = 1,3   m m , calcule a máxima tensão de cisalhamento em Pa.

Passo 1

Tá legal, na condição descrita no enunciado, podemos utilizar a equação 8.7 vista nesse capítulo, dada por:

u = a 2 2 μ ∂ p ∂ x y a 2 - 1 4

E, conforme vimos, devemos considerar a coordenada inicial em y como sendo a linha de centro do escoamento. Agora, sabemos também que a tensão de cisalhamento será dada por:

τ y x = μ . d u d y

Então, precisamos encontrar a expressão para a derivada da velocidade com relação a y . Então, teremos:

d u d y = a 2 2 μ ∂ p ∂ x 2 y a 2 → d u d y = y μ ∂ p ∂ x

Então, substituindo essa expressão na equação de cima, temos:

τ y x = μ y μ ∂ p ∂ x → τ y x = y . ∂ p ∂ x

Passo 2

Agora, analisando a expressão obtida no passo 1, sabemos que quando temos u > 0 → ∂ p ∂ x > 0 , então, com relação a y , temos:

y > 0 → τ y x > 0

y < 0 → τ y x < 0

Dessa forma o gráfico dessa função será negativo para y < 0 e positivo para y > 0 , e linear, então, teremos:

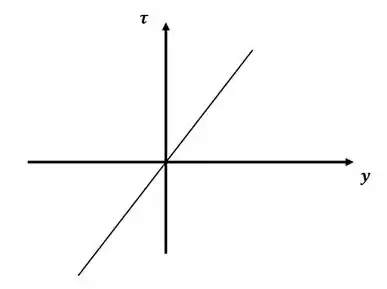
Passo 3

E, sabemos que a tensão de cisalhamento máxima ocorre na parede (outra coisa que podemos confirmar através do gráfico do passo 2), então, para y = h / 2 temos:

τ y x m a x = y ∂ p ∂ x

Então, substituindo os valores conhecidos, temos:

τ y x m a x = h 2 ∂ p ∂ x = 1,3.10 - 3 2 58 → τ y x m a x = 3,77.10 - 2   P a / m

E, para y = - h / 2 , teremos o mesmo valor em módulo, só que com sinal negativo.

Resposta

τ y x = y . ∂ p ∂ x

τ y x m a x = 3,77.10 - 2   P a / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema na Figura P6.105 consiste em 1.200 m de tubo de ferro fundido de 5 cm de diâmetro, dois cotovelos de 45 ° e quatro de 90 ° , flangeados e de raio longo, uma válvula globo flangeada completam
Uma bomba com rendimento de 70% fornece água a 20 ° C de um reservatório para outro 6,1 metros mais alto, como na Figura P6.102. O sistema de tubulação consiste em 18,3 m de tubo de aço galvanizado de
A figura a seguir, tem a entrada do tubo como um canto vivo. Se a vazão é de 0,004 m³/s, qual a potência, em W, extraída pela turbina?
A bomba d’água na figura abaixo mantém uma pressão de 45 kN/m² no ponto 1. Há um filtro, uma válvula de disco aberta pela metade e dois cotovelos normais rosqueados. Há 24 m de tubo de aço comercial d
Na figura abaixo o tubo é de aço galvanizado. Calcule o percentual de aumento na vazão (a) se a entrada do tubo for cortada rente à parede do reservatório e (b) se a válvula borboleta estiver totalmen