41 – Um aquecedor de água de alimentação, que abastece uma caldeira, é constituído por um trocador de calor casco e tubos com um passe no casco e dois passes nos tubos. Ele tem cem tubos com paredes delgadas, diâmetro de e comprimento (por passe) de . Sob condições normais de operação, a água entra nos tubos com uma vazão total de e a , sendo aquecida pela condensação de vapor de água saturado a sobre a superfície externa dos tubos. O coeficiente de transferência de calor no lado do vapor saturado é de .
(a) Determine a temperatura de saída da água.
(b) Com todas as demais condições permanecendo inalteradas, porém levando em consideração variações no coeficiente global de transferência de calor, represente graficamente a temperatura de saída da água como uma função de sua vazão para .
(c) No gráfico da parte (b), adicione duas curvas para a temperatura de saída da água como uma função de sua vazão para fatores de deposição de e .
Passo 1
Repare a ilustração para melhorar seu entendimento.
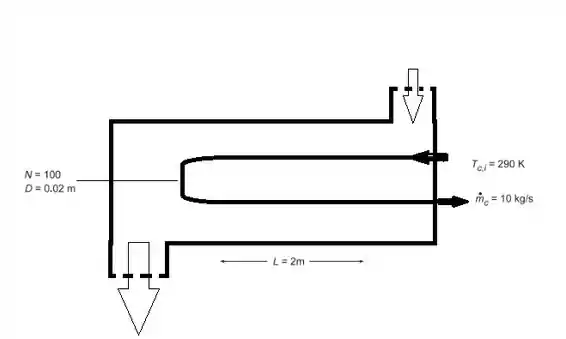
Passo 2
a) Como precisamos encontrar o coeficiente convectivo, teremos que encontrar o número de Reynolds para depois encontrar o número de Nusselt e por fim acharmos o coeficiente.
Portanto, o número de Reynold para um tubo pode se encontrado por meio da seguinte relação:
Aqui, é vazão mássica, é o número de tubos, é o diâmetro e a é a viscosidade.
Como o número , o fluxo de água é turbulento e totalmente desenvolvido.
Passo 3
Podes calcular o número de Nusselt para o tubo por meio da seguinte equação.
Aqui, é o número prandtl.
Obtenha o número de prandtl na tabela A.6, “Propriedades termo físicas da água à pressão atmosférica”. Em uma temperatura de .
Logo:
Passo 4
Finalmente podemos calcular o coeficiente de transferência de calor por convecção na superfície interna do tubo, por meio da seguinte relação.
Reescreva para achar :
Portanto, o coeficiente de convecção do fluxo do tubo é .
Passo 5
Agora precisamos do coeficiente geral de transferência de calor que é fornecido por:
Aqui, é o coeficiente de transferência de calor por convecção na superfície interna do tubo e é o coeficiente de transferência de calor por convecção na superfície externa do tubo.
![]()
Portanto, o coeficiente geral de transferência de calor é .
Passo 6
Vamos calcular a área da superfície do trocador de calor de fluxo cruzado, usando a equação a seguir.
Passo 7
Precisamos também da taxa de capacidade de calor para fluido frio, que é dada por:
Aqui, é a taxa mínima de capacidade de aquecimento.
Passo 8
Temos que o NTU (número de unidades de transferência) é usado para calcular a taxa de transferência térmica em trocadores de calor. Em termos de coeficiente geral de transferência de calor é dado por,
Aqui, é o coeficiente geral de transferência de calor, é a área de superfície do trocador de calor de fluxo cruzado e a taxa de capacidade de calor mínima.
Passo 9
A eficácia pode ser encontrada por meio da equação a seguir.
Passo 10
Vamos agora calcular a taxa máxima de transferência de calor possível.
Aqui, é a temperatura de entrada do ar do fluido frio e a é a temperatura de entrada do fluido quente.
Passo 11
A taxa de transferência de calor é dada por:
Passo 12
E para finalizar, vamos calcular a temperatura da saída de ar.
Aqui, é a taxa de transferência de calor, é a temperatura da entrada de ar e é a taxa de capacidade de calor para o ar fluido frio.
Portanto, a temperatura de saída da água é .
Resposta
- É necessário o uso de software (IHT).
- É necessário o uso de software (IHT).