47 - Considere um trocador de calor bitubular muito comprido com temperaturas de entrada da água quente e da água fria de e . A vazão da água quente é duas vezes a da água fria. Considerando calores específicos equivalentes para a água quente e a água fria, determine a temperatura de saída da água quente para as seguintes modalidades de operação: (a) escoamento em contracorrente e (b) escoamento em paralelo.
Passo 1
Vamos listar os dados conhecidos:
• Trocador de calor de tubo concêntrico com fluido quente como água quente e fluido frio como água fria.
• A temperatura de entrada de água fria é
• A temperatura de entrada de água quente é .
• A vazão da água quente é
Passo 2
Segue a ilustração do trocador de calor.
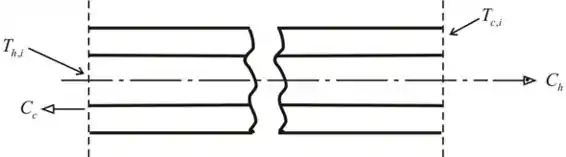
Passo 3
Precisamos adotar algumas condições para prosseguir:
• A perda de calor nos arredores é insignificante.
• As propriedades são assumidas como constantes.
Análise:
a) Temperatura de saída da água quente para o modo de operação de contracorrente:
Pela aplicação do balanceamento de energia geral ao fluido quente e frio da Equação 11.11, temos:
Transferência de calor = Calor perdido pelo fluido quente = Calor ganho pelo fluido frio
Onde,
Como foi dito que a vazão de uma é duas vezes a outra, temos então:
Passo 4
Como :
Para um trocador de calor de tubo concêntrico longo com uma grande área de superfície operando sob condições de contracorrente, a taxa de transferência de calor é dada por:
Temos então que a taxa de transferência de calor é:
Da equação temos:
Substituindo pelos resultados obtidos.
Portanto, a temperatura de saída da água quente para o escoamento em contracorrente é .
Passo 5
b) Temperatura de saída da água quente para o escoamento em paralelo:
Para o escoamento em paralelo, a temperatura de saída da água fria é e a temperatura de saída da água quente são iguais, ou seja,
Igualando ambas transferências de calor para os dois fluidos, temos:
Portanto, a temperatura de saída da água quente para o escoamento paralelo é .