44 - Vapor de água saturado deixa uma turbina a vapor a uma vazão de e a uma pressão de . O vapor deve ser completamente condensado em líquido saturado em um trocador de calor casco e tubos que usa água da rede pública como fluido frio. A água entra nos tubos, com paredes delgadas, a e deve deixá-los a . Supondo um coeficiente global de transferência de calor de , determine a área da superfície de transferência de calor necessária e a vazão de água. Após um longo período de operação, a deposição causa uma diminuição no coeficiente global de transferência de calor para , de modo que para condensar completamente o vapor deve haver uma redução na sua vazão. Para as mesmas temperaturas de entrada e vazão da água, qual é a nova vazão de vapor necessária para uma condensação completa?
Passo 1
Vamos considerar a figura a seguir, mostrando a disposição da turbina e do trocador de calor:
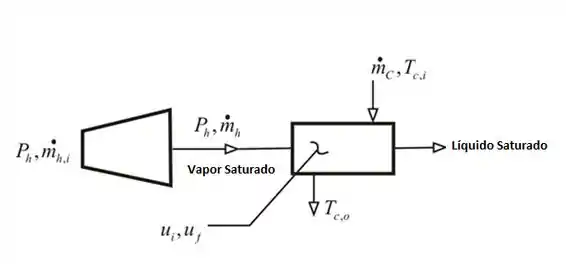
Passo 2
a)Vamos aplicar comigo o balanço de energia para esse trocador de calor.
O calor perdido pelo fluido quente deve ser igual ao calor ganho pelo fluido frio, logo:
Para prosseguir, precisaremos obter alguns valores tabelados. Para a água quente a uma temperatura de saturação e pressão de , temos na tabela A.6, “Propriedades termo físicas da água saturada” os seguintes dados:
Calor de vaporização é:
Portanto, voltando a equação obtemos:
Passo 3
Agora, vamos precisar calcular a temperatura média do fluido frio, que pode ser obtida como:
Novamente, vamos obter as seguintes propriedades da água a na tabela A.6, “Propriedades termofísicas da água saturada” no livro.
Calor específico de fluido frio é:
Calcular a capacidade de calor do fluido frio como:
Vamos fazer uma substituição na equação usando a .
Substituindo pelos valores conhecidos, temos:
Portanto, a taxa de fluxo do fluido frio é .
Logo, a capacidade térmica do fluido frio é dada por:
Passo 4
Observe que temos a seguinte relação:
Dessa forma a taxa de capacidade térmica é dada como,
.
Temos que a eficácia é a razão entre a taxa real de transferência de calor e a taxa máxima de transferência de calor, como mostrado abaixo:
A taxa máxima de transferência de calor pode ser determinada de imediato pela expressão seguinte expressão.
Aqui, é a temperatura de entrada do fluido quente e é a temperatura de saída do fluido frio.
Substituindo pelos valores conhecidos, obtemos:
Passo 5
Temos que o NTU (número de unidades de transferência) é usado para calcular a taxa de transferência térmica em trocadores de calor. Fornecido por meio da seguinte equação:
Como nosso a equação se transforma em:
Substituindo pelo valor da eficácia, temos:
Agora que temos todos os dados, podemos obter a área por meio de uma outra expressão usada para achar , que segue abaixo:
Portanto, a área de superfície necessária para o trocador de calor é .
Passo 6
b)Agora, vamos repetir os passos anteriores, porém temos que diminuir o coeficiente de transferência de calor geral por conta das instruções do enunciado.
Agora, para encontramos o valor da eficácia vamos utilizar a equação .
Portanto a nova taxa de transferência de calor pode ser obtida usando a relação a seguir,
E por fim, a nova vazão mássica com incrustação pode ser obtida por meio da equação .
Portanto, a vazão de massa necessária para a condensação completa quando ocorre incrustação é .