Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 75
75 - Considere o Problema 1.1.
(a) Estando a superfície fria exposta do isolante a , qual é o valor do coeficiente de transferência de calor por convecção no lado frio do isolante, se a temperatura da vizinhança for de, a temperatura ambiente e a emissividade ? Expresse o
seu resultado nas unidades e .
(b) Usando o coeficiente de transferência de calor por convecção calculado no item (a), calcule a temperatura superficial, , na medida em que a emissividade da superfície é variada na faixa. A temperatura da parede quente do isolante permanece fixa a . Apresente os seus resultados graficamente.
Passo 1
a)
A transferência de calor na superfície fria ocorre devido a
1. Condução de calor do lado quente para o lado frio
2. Ganho de calor devido à radiação
3. Perda de calor devido a convecção
Para transferência de calor em estado estacionário
Calor ganho = calor perdido
Calor ganho por radiação + Calor ganho por condução = Calor perdido por convecção
Portanto, o coeficiente de convecção é .
Passo 2
b)
Da relação para transferência de calor em estado estacionário,
Ao resolver a equação acima no computador, obtemos o gráfico abaixo.
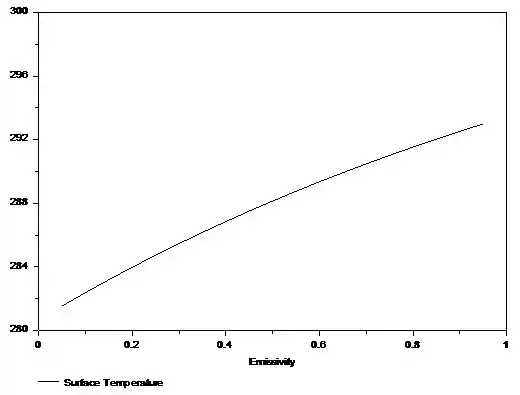
À medida que a emissividade aumenta, a temperatura da superfície aumenta. Assim, a radiação aquece a superfície.
