Um carregador de telefone celular com 50 mm × 45 mm × 20 mm tem uma temperatura superficial de Ts = 33°C, quando ligado a uma tomada elétrica, sem estar em uso. A superfície do carregador tem emissividade ε = 0,92 e está submetida a um coeficiente de transferência de calor por convecção natural h = 4,5 W/(m2 · K). A temperatura do ar no ambiente e a temperatura da vizinhança são = 22°C e = 20°C, respectivamente. Sendo os custos da eletricidade iguais a C = $0,18/(kW · h), determine o custo diário de manter o carregador ligado na tomada, sem estar em uso.
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Primeiro, vamos ver o esquema do carregador:
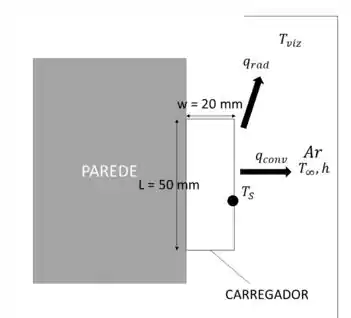
O carregador está trocando calor com o ambiente externo por convecção e radiação por 5 de seus 6 lados, exceto o que está colado na parede, como mostra a figura.
Esse problema quer que você descubra o custo de manter o carregador ligado na tomada sem estar em uso, a partir do conhecimento da taxa de energia dissipada na forma de calor , que pode ser entendida como uma soma da dissipação por convecção e por radiação.
Sendo assim, o balanço de energia para a superfície do carregador é:
Antes de irmos ao passo 2, quero deixar aqui algumas propriedades e grandezas que vamos utilizar no problema e quero que você se lembre:
Passo 2
Agora vou mostrar as equações que vamos utilizar para calcular as taxas convectiva e radiante:
A área , como eu te disse no Passo 1, é uma soma das áreas de 5 dos seis lados do carregador:
Para calcular a taxa convectiva, basta substituir as grandezas dadas pelo enunciado e a área que acabamos de calcular:
Já para calcular a taxa de emissão por radiação, devemos substituir a emissividade dada pelo problema, a constante de Stefan-Boltzmann (σ = ), área e as temperaturas da superfície e da vizinhança. Lembre que para calcular taxas radiantes, devemos colocar as temperaturas em Kelvin!
Substituindo estes valores no balanço deduzido no Passo 1, podemos encontrar a taxa de energia dissipada na forma de calor:
Passo 3
Agora, podemos calcular o custo diário para manter o carregador na tomada:
Resposta
Como demonstrado no Passo 3, o custo é de .