Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 59
Considere a turbina eólica do Exemplo 1.3. Para reduzir a temperatura no envoltório cilíndrico da turbina para Ts = 30°C é aberta uma comunicação com o exterior e um ventilador instalado para forçar a circulação do ar em seu interior. Qual é a vazão mássica mínima de ar necessária no caso de sua temperatura chegar à temperatura da superfície interna do envoltório antes de deixar o ambiente interno? O calor específico do ar é de 1007 J/(kg · K).
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Primeiro, vamos ver o esquema da turbina:
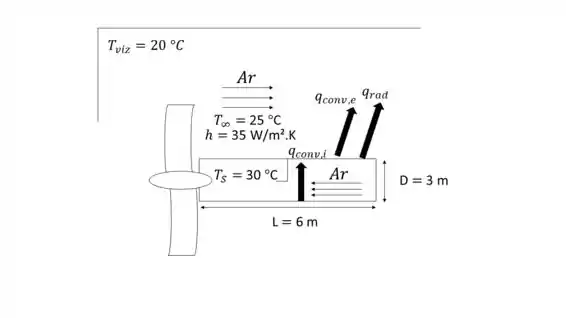
A turbina pode ser modelada como um cilindro trocando calor com o ambiente externo por convecção e radiação ao longo de toda sua área superficial e em uma de suas bases.
Para manter a temperatura da superfície do envoltório em 30 , uma corrente de ar circula dentro da turbina, proporcionando uma transferência de calor por convecção interna.
Além disso, da questão anterior, sabemos que a soma das energias mecânica e elétrica necessárias para a turbina funcionar é .
Esse problema quer que você descubra a vazão mássica dessa corrente de ar na parte interna da turbina, a partir do conhecimento da taxa de transferência de calor por convecção interna .
Sendo assim, o balanço de energia para a superfície da turbina é:
Antes de irmos ao passo 2, quero deixar aqui algumas propriedades e grandezas que vamos utilizar no problema e quero que você se lembre:
Passo 2
Agora vou mostrar as equações que vamos utilizar para calcular as taxas convectiva externa e radiante:
A área , como eu te disse no Passo 1, é uma soma da área superficial e da área uma das bases do cilindro. Dessa forma, podemos calculá-la como:
Para calcular a taxa convectiva, basta substituir as grandezas dadas pelo enunciado e a área que acabamos de calcular:
Já para calcular a taxa de emissão por radiação, devemos substituir a emissividade dada pelo problema, a constante de Stefan-Boltzmann (σ = ), área e as temperaturas da superfície e da vizinhança. Lembre que para calcular taxas radiantes, devemos colocar as temperaturas em Kelvin!
Substituindo estes valores no balanço deduzido no Passo 1, podemos encontrar a taxa de transferência de calor por convecção interna:
Passo 3
Agora, podemos calcular a vazão mássica de ar a partir da equação:
Resposta
Como demonstrado no Passo 3, a vazão mássica de ar é .