Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 12.Problemas - Ex. 94

A absortividade espectral de uma superfície opaca é como mostra a figura abaixo. Determine a absortividade da superfície para radiação emitida por uma fonte de a (a) 1000 K e (b) 3000 K.

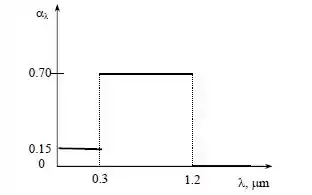
Passo 1

(a) Para T=1000K a gente vai partir do princípio que a absortividade média é calculada da seguinte forma:

α T = α 1 f λ 1 + α 2 f λ 2 - f λ 1 + α 3 1 - f λ 3

Onde cada uma dessas funções f são tabeladas de acordo com o valor da expressão de λ i T de cada intervalo do gráfico, se liga!

λ 1 T = 0,3 1000 = 300 μ m K → f λ 1 = 0

λ 2 T = 1,2 1000 = 1200   μ m K → f λ 2 = 0,002134

Portanto,

α T = 0,15 0,0 + 0,7 0,002134 - 0 + 0 1 - 0,002134

α T = 0,00149

Passo 2

(b) Para T = 3000K

α T = α 1 f λ 1 + α 2 f λ 2 - f λ 1 + α 3 1 - f λ 3

Onde cada uma dessas funções f são tabeladas de acordo com o valor da expressão de λ i T de cada intervalo do gráfico, se liga!

λ 1 T = 0,3 3000 = 9 00 μ m K → f λ 1 = 0 , 000169

λ 2 T = 1,2 3 000 = 3600   μ m K → f λ 2 = 0,403607

Portanto,

α T = 0,15 0,0 00169 + 0,7 0,403607 - 0 , 000169 + 0 1 - 0,403607

α T = 0,282

Resposta

  1. α = 0,00149
  2. α = 0,282
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Defina as propriedades emissividade e absortividade. Quando essas duas propriedades são iguais?
A superfície do Prob 12-94 recebe radiação solar a uma taxa de 470 W/m². Determine a absortividade solar da superfície e taxa de absorção da radiação solar.
A radiação solar incide sobre a superfície frontal de uma placa fina com componentes direto e difuso de 300 e 250 W/m², respectivamente. A radiação direta faz um ângulo de 30° com a normal da superfíc
A emissividade espectral de uma superfície opaca a 1200 K é aproximada como ε 1 = 0 , p a r aλ2μ m ε 2 = 0,85 p a r a2 ≤ λ ≤ 6μ m ε 3 = 0p a r aλ6μ m Determine a emissividade total e o fluxo emissivo