Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 12.Problemas - Ex. 91

A emissividade espectral de uma superfície opaca a 1200 K é aproximada como

ε 1 = 0 ,                     p a r a   λ < 2   μ m

                ε 2 = 0,85             p a r a   2 ≤ λ ≤ 6   μ m    

ε 3 = 0                       p a r a   λ > 6   μ m      

Determine a emissividade total e o fluxo emissivo da superfície.

Passo 1

Nesse tipo de exercício, o primeiro passo que eu te recomendo (MUITOOOO) a desenhar como seria essa função, se liga!

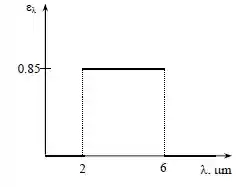
Passo 2

A gente sabe que a emissividade média da superfície pode ser determinada como:

ε T = ε 1 f λ 1 + ε 2 f _ λ 2 - f _ λ 1 + ε 3 ( f _ λ 3 - f _ λ 2 )

Onde todos esses f são fatores correspondentes a um produto entre o comprimento de onda correspondente e a temperatura, que serão funções determinadas na tabela 12-2 do livro.

λ 1 T = 2 1200 = 2400   μ m K → f λ 1 = 0,140256

λ 2 T = 6 1200 = 7200   μ m K → f λ 2 = 0,819217

Resumidamente: você calcular esse produto aí do lado esquerdo, e depois com esse valor, vai na tabela que eu comentei pra ti e ver quanto vale a função de lâmbda, beleza?

Passo 3

Portanto, utilizando a fórmula do início do passo 2:

ε = 0 0,140256 + 0,85 0,819217 - 0,140256 + 0 1 - 0,819217

ε = 0,5771

E o fluxo emissivo será dado por:

E = ε σ T 4 = 0,5771 5,67 x 10 - 8 1200 = 67850   W / m ²

Resposta

ε = 0,5771

E = 67850   W / m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Radiação deixa um forno, que tem temperatura superficial interna de 1500K , através de uma abertura com 20m m de diâmetro. Uma porção dessa radiação é interceptada por um detector que se encontra a um
As transmissividades espectrais de vidros simples e vidros coloridos podem ser aproximadas como a seguir:Fora dos intervalos de comprimentos de onda especificados, a transmissividade espectral para os
A emissividade espectral de uma superfície difusa e opaca é mostrada na figura.(a) Se a superfície for mantida a 1000K , qual é sua emissividade hemisférica total?(b) Qual é a absortividade hemisféric
Considere um material que é cinza, mas seletivo direcionalmente com α θ θ ,ϕ = 0,5 1–c o s ϕ . Determine a absortividade hemisférica α quando um fluxo solar colimado irradia a superfície do material n
Quatro superfícies difusas, que apresentam as características espectrais mostradas nas figuras, se encontram a 300 K e estão expostas à radiação solar.Quais das superfícies podem ser aproximadas como