Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 20

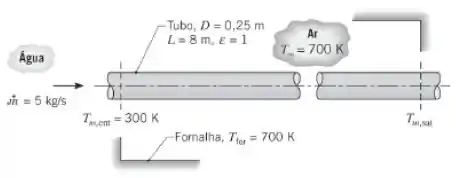
Água, a 300 K e com uma vazão de 5 k g s , entra em um tubo de parede delgada preta, que atravessa uma grande fornalha cujas paredes e o ar estão a uma temperatura de 700 K. O diâmetro e o comprimento do tubo são de 0,25 m e 8 m, respectivamente. Os coeficientes convectivos associados ao escoamento da água no interior do tubo e do ar sobre sua superfície externa são 300 W m 2 K e 50 W m 2 K , respectivamente.

  1. Escreva uma expressão para o coeficiente radiante linearizado correspondente à troca radiante entre a superfície externa do tubo e as paredes da fornalha. Explique como calcular esse coeficiente se a temperatura da superfície do tubo for representada pela média aritmética dos seus valores na entrada e na saída do tubo.
  2. Determine a temperatura da água na saída do tubo, T m , s a i .

Passo 1

Faaaaaaaaaaaaalaa galerinha!!

Bora continuar?!

A letra (a) nos pede para escrever uma expressão para o coeficiente radiante linearizado correspondente à troca radiante entre a superfície externa do tubo e as paredes da fornalha.

Fazendo o balanço de energia:

q c o n v ,   i = q c o n v ,   e + q r a d

Substituindo o calor em função da variação da temperatura sobre a resistência:

T m - T t - R c o n v ,   i = T t - - T f o r n o R c o n v ,   e + T t - - T f o r n o R r a d

Onde T t - é a temperatura média da parede do tubo e T m a temperatura média do fluido!

T m - T t - R c o n v ,   i = T t - - T f o r n o 1 R c o n v ,   e + 1 R r a d

Lembrando que as resistências são calculadas como:

R c o n v ,   i = 1 h   i A s

R c o n v ,   e = 1 h   e A s

R r a d = 1 h r a d - A s

Substituindo:

h   i A s T m - T t - = T t - - T f o r n o h   e A s + h r a d - A s

h r a d - = h   i T m - T t - T t - - T f o r n o - h   e

E quando:

T m = T m , e n t + T m , s a i 2

O coeficiente radioativo ficará assim:

h r a d - = h   i T m , e n t + T m , s a i - 2 T t - 2 T t - - T f o r n o - h   e

Passo 2

Na letra (b) nós queremos a temperatura na saída do tubo!

Aqui vamos lembrar que a variação de temperatura da saída e da entrada com relação ao ambiente, no caso o forno, também podem ser calculadas em função da resistência, de acordo com a equação 8.45b:

T f o r n o - T m , s a i T f o r n o - T m , e n t = e - 1 m ˙ c p R T

T m , s a i = T f o r n o - T f o r n o - T m , e n t e - 1 m ˙ c p R T

Nós sabemos que:

m ˙ = 5 k g s

T f o r n o = 700   K

T m , e n t = 300   K

T t - = 304   K

Para a temperatura média T t - próximo de 304 K a tabela A.6 nos diz que:

c p = 4178 J K g K

Como as resistências externas estão em paralelo entre elas e em série com a resistência interna, a resistência total será calculada como:

R T = R c o n v ,   i + 1 1 R c o n v ,   e + 1 R r a d

Melhor calcularmos cada uma separadamente, certo?

R c o n v ,   e = 1 h   e π D L = 1 50 W m 2 K π × 0,25   m × 8   m = 3,18 × 10 - 3 K W

R c o n v ,   i = 1 h   i π D L = 1 30 0 W m 2 K π × 0,25   m × 8   m = 5,31 × 10 - 4 K W

Para a resistência a radiação precisamos do coeficiente linearizado, assumimos que ε = 1 :

h r a d - = 5,67 × 10 - 8 W m 2 K 4 304   + 700 304 2 - 700 2 K 3

h r a d - = 33,15 W m 2 K  

E agora a resistência:

R r a d = 1 33,15 W m 2 K π × 0,25   m × 8   m = 4,80 × 10 - 3 K W

Calculando a resistência total:

R T = 5,31 × 10 - 4 K W + 1 1 3,18 × 10 - 3 K W + 1 4,80 × 10 - 3 K W

R T = 2,44 × 10 - 3 K W

Com a resistência total nós podemos calcular a temperatura de saída:

T m , s a i = 700   K - 700   K - 300   K e - 1 5 k g s × 4178 J K g K × 2,44 × 10 - 3 K W

T m , s a i = 308   K

Portanto, valida a nossa afirmação de que T t - = 304   K !!

Essa foi legal, não foi?

Resposta

  1. h r a d - = h   i T m - T t - T t - - T f o r n o - h   e     |     h r a d - = h   i T m , e n t + T m , s a i - 2 T t - 2 T t - - T f o r n o - h   e ;
  2. T m , s a i = 308   K .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água, a uma vazão = 0,215 kg/s, é resfriada de 70°C para 30°C pela sua passagem através de um tubo de parede delgada e diâmetro D = 50 mm, sobre o qual um refrigerante a T∞ = 15°C é mantido em escoame
Repita o Problema 8.66 para um tubo circular de diâmetro D = 2 mm, um fluxo imposto de q ″=200.000W / m 2 , e uma vazão mássica de m = 10 g/s.
Um tubo circular de diâmetro D = 0,2 mm e comprimento L = 100 mm impõe um fluxo térmico constante de q″ = 20 × 103 W/m2 em um fluido que escoa a uma vazão mássica de = 0,1 kg/s. Para uma temperatura n
Seja um tubo metálico de parede delgada, com comprimento L = 1 m e diâmetro interno Di = 3 mm. Água entra no tubo a uma vazão m = 0,015 kg/s e Tm,ent = 97°C. (a) Qual é a temperatura de saída da água
Com o objetivo de manter as exigências de potência de bombeamento por unidade de vazão abaixo de um nível aceitável, a operação do oleoduto do Problema 8.63 está sujeita à restrição de que a temperatu