Considere o desenvolvimento de uma camada-limite térmica laminar próxima a entrada do tubo mostrado na Figura 8.4. Quando a camada-limite fluidodinâmica é fina em relação ao diâmetro do tubo, a região de escoamento invíscico tem uma velocidade uniforme que é aproximadamente igual à velocidade média . Assim, o desenvolvimento da camada-limite é
similar ao que ocorre em uma placa plana.
- Partindo da Equação 7.23, deduza uma expressão para o número de Nusselt local, , como uma função do número de Prandtl, Pr, e do inverso do número de Graetz, . Represente graficamente a expressão usando as coordenadas mostradas na Figura 8.10a, para Pr = 0,7.
- Partindo da Equação 7.30, deduza uma expressão para o número de Nusselt médio, , como uma função do número de Prandtl, Pr, e do inverso do número de Graetz, . Compare os seus resultados com o número de Nusselt para comprimento de entrada combinada no limite de pequenos x.
Passo 1
Boom galerinhaa, vamos continuar ?!
Na letra (a) nos foi pedido para usar a Equação 7.23 e deduzir uma expressão para o número de Nusselt local, , como uma função do número de Prandtl, Pr, e do inverso do número de Graetz, .
Relembrando a equação 7.23:
Para transformar em nós vamos ter que multiplicar ambos os lados por
E lembrando que:
Então:
Agora nós vamos ter que lançar mão de alguns artifícios matemáticos:
Vamos substituir?
Olha que legal!!
Sabendo que:
Em função de
Passo 2
A letra (a) ainda não acabou, certo? Queremos saber o número de Nusselt quando e quando varia conforme a figura 8.10ª, ou seja, de 0,001 até 1.
Vamos obter os seguintes valores:
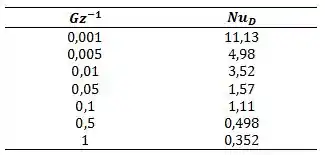
Colocando no gráfico:
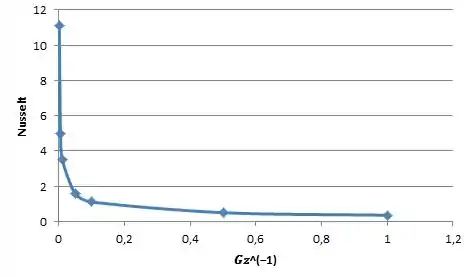
Passo 3
Na letra (b) nos foi pedido para usar a Equação 7.30 e deduzir uma expressão para o número de Nusselt médio, , como uma função do número de Prandtl, Pr, e do inverso do número de Graetz, .
Relembrando a equação 7.30:
Para transformar em nós vamos ter que multiplicar ambos os lados por
E lembrando que:
Então:
Agora nós vamos ter que lançar mão de alguns artifícios matemáticos:
Vamos substituir?
Sabendo que:
Em função de
Passo 4
A letra (b) ainda não acabou, certo? Queremos saber se os este resultado é compatível com o número de Nusselt para comprimento de entrada combinada no limite de pequenos x.
Lembrando que o número médio de Nusselt para o comprimento da entrada é dado como:
Quando é muito pequeno, também é!! Também podemos observar que
É importante lembrar da matemática que quando
Assumindo que
Bem próximo, não é?!
Resposta
