Um tubo circular de diâmetro D = 0,2 mm e comprimento L = 100 mm impõe um fluxo térmico constante de q″ = 20 × 103 W/m2 em um fluido que escoa a uma vazão mássica de = 0,1 kg/s. Para uma temperatura na entrada de Tm,ent = 29°C, determine a temperatura na parede do tubo em x = L para o fluido sendo água pura. Avalie as propriedades do fluido a = 300 K. Para as mesmas condições, determine a temperatura da parede do tubo em x = L para o fluido sendo o nanofluido do Exemplo 2.2.
Passo 1
Beleza galerinha, vamos lá! O número Reynolds para a água pura, é 745. e o fluxo é laminar. Da mesma forma, o número Reynolds para o nanofluido é ReD,nf = 662. O comprimento de entrada hidrodinâmica para a água pura é xfd,h = 0,05ReDD = 0,05 × 745 × 0,2/1000 m = 7,45 × 10-3 m = 7,45 mm e o fluxo na saída do tubo é hidrodinâmico totalmente desenvolvido. Similarmente, o comprimento de entrada hidrodinâmica para o nanofluido é xfd,h,nf = 6,62 × 10-3 m = 6,62 mm e o fluxo na saída do tubo também está totalmente desenvolvido hidrodinamicamente. Para a água pura, o comprimento de entrada térmica é xfd,t = xfd,hPr bf= 7,45 mm × 5,83 = 43,4 mm, enquanto para o nanofluido xfd,t ,nf= xfd,h,nfPrnf= 6,62 mm × 4,91 = 32,5 mm e o fluxo também está completamente desenvolvido termicamente na saída do tubo para ambos os fluidos.
Passo 2
Para condições de fluxo de calor constante, o número Nusselt local na região totalmente desenvolvida é NuD = 4,36. Aplicação de Eq. (8,40) no rendimento de fluidos puros,
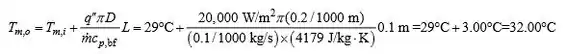
enquanto a aplicação de Eq. (8,40) ao nanofluido resulta em,
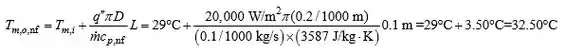
Passo 3
A partir de Eq. (8,27) a temperatura da parede na saída do tubo que transporta a água pura é,,
![]()
Da mesma forma para o nanofluido,
