Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 97
Água escoa a 25 L/s através de uma constrição suave, em que o diâmetro do tubo é reduzido de 75 mm para 37,5 mm, segundo um ângulo de 150°. Se a pressão antes da constrição for 500 kPa, estime a pressão depois da constrição. Refaça o problema se o ângulo da constrição for 180° (uma constrição brusca).
Passo 1
Neste problema é pedido a pressão após uma constrição. Para isso será utilizada a Equação da Energia, em J/kg, ao longo do trecho com constrição, conforme Figura abaixo:
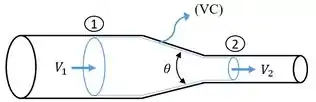
Será utilizada a equação na forma:
Sendo a perda de carga menor (da constrição) definida como:
Como hipótese e dados do enunciado tem-se que;
- regime permanente ();
- escoamento horizontal ();
- escoamento incompressível ( e );
- ;
- ;
- ;
- ;
- ;
- .
Passo 2
Usando a Equação de Energia, em J/kg, entre as seções 1 e 2:
Sabendo a expressão de , que e
Passo 3
Conehcendo a vazão do escoamento, é possível escrever as velocidades em função da vazão:
Então na seção 1:
Na seção 2:
Passo 4
Reescrevendo a expressão de com as expressões de e :
Passo 5
Sabendo que a relação de áreas é dada por:
Então pela Tabela 8.3 e conhecendo e , o coeficiente de perda de carga para a constrição vale:
Passo 6
Calculando a partir dos dados conhecidos:
Então, vale:
Passo 7
Considerando que a constrição tenha , o coeficiente de perda de carga para essa nova situação será:
E pressão será calculada da forma:
Então, para a pressão vale:
Resposta
- Para :
- Para :