Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 2

Qual é o significado típico do número de Reynolds? Como ele é definido para :

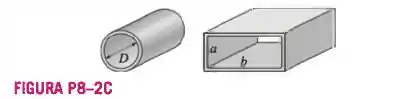
  1. fluxo em um tubo circular de diâmetro interno D  
  2. fluxo em um duto retangular de seção transversal a   X   b

Passo 1

O número de Reynolds é a razão entre as forças inerciais e as forças viscosas a gente usa ele bastate para saber se o um fluxo é laminar ou turbulento!

R e = f o r ç a s   i n e r c i a i s f o r ç a s   v i s c o s a s

Quando o número de Reynolds é alto, isso significa que as forças de inerciais são muito maiores que as forças viscosas, nesse caso o regime é turbulento!

Quando o número de Reynolds é baixo o que acontece é o contrário, as forças viscosas são maiores.

Para a gente entender isso melhor, imagina o mel, ele tem viscosidade alta e é bem difícil imaginar o mel em um escoamento turbulento! Certo?!

Passo 2

Agora vamos ver como calcula o número de Reynolds nos dois casos que o enunciado pediu!

  1. fluxo em um tubo circular de diâmetro interno D  

R e = ρ V D μ

Onde ρ ,   V , D   e   μ são respectivamente a densidade do fluido, a velocidade do escoamento, o diâmetro da secção trasnversal por onde o fluido escoa e a viscosidade dinâmica

Passo 3

  1. fuxo em um duto retangular de seção transversal a   X   b

R e = ρ V D h μ

Aqui o que tem de diferente é esse D h , ele é o diâmetro hidraulico, dado por:

D h = 4   A c p

A c é a área de secção transversal, que como aqui é retangular é dada por:

A c = 2 a b

E p é o perimetro da secção transversal:

p = 2 × ( a + b )

Juntando isso, temos:

D h = 2 a b a + b

Resposta

(a) R e = ρ V D μ

(b) D h = 2 a b a + b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor elétrico fornece 3 kW à bomba da instalação da figura, que tem um rendimento de 80%. Sendo dados:a) as tubulações são de mesma seção, cujo diâmetro é de 5 cm e de mesmo material;b) k s 1 = 10
Numa certa região, há três reservatórios naturais, A, B e C, e um conjunto TB formado por uma turbina acoplada diretamente a uma bomba. As perdas de carga nas tubulações são:Entre a e b, H p a , b = 0
Calcular a vazão na tubulação da figura para H = 10m . Calcular em seguida o novo valor de H para que a vazão seja 50L / s . Dados: D = 150m m ;ν = 1,05.10 - 6m 2 / s ; γ = 10 4N / m 3 ; k = 25,9.10 -
Dada a instalação da figura, determinar a pressão p 0 para que a vazão seja 6 L/s. Em seguida, traçar a linha piezométrica e a linha de energia sobre a instalação, marcando o valor das respectivas alt
Água escoa em regime laminar num conduto cilíndrico horizontal de diâmetro D. A linha de energia forma com a horizontal um ângulo α . Determinar a vazão. Dados: ν = 10 - 6m 2 / s ; D = 1c m ; tg ⁡ α =