Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 78

Água está escoando em regime permanente por um cotovelo de 180 ° . Na entrada do cotovelo, a pressão manométrica é 103   k P a . A água é descarregada para a atmosfera. Considere que as propriedades são uniformes nas seções de entrada e de saída; A 1 = 2500   m m 2 , A 2 = 650   m m 2 e V 1 = 3   m / s . Determine a componente horizontal da força necessária para manter cotovelo no lugar.

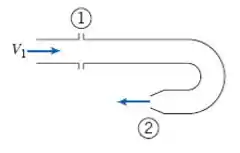
Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante;
  4. Escoamento uniforme.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não temos a variação das propriedades com o tempo nem força de campo atuando, então:

∂ ∂ t = 0

Assim, F S x = R x :

R x + P 1 A 1 = ∫ S C u ( ρ V ) d A

Passo 3

R x + P 1 A 1 = ∫ S C u ( ρ V ) d A

R x + P 1 A 1 = u 1 - ρ V 1 A 1 - u 2 ρ V 2 A 2

Sendo:

u 1 = V 1 ;

u 2 = V 2 ;

Temos:

R x = - P 1 A 1 - ρ V 1 2 A 1 - ρ V 2 2 A 2

R x = - P 1 A 1 - ρ ( V 1 2 A 1 + V 2 2 A 2 )

Passo 4

Dados:

V 1 = 3   m / s ;

A 1 = 2500   m m 2 = 0,0025   m 2 ;

  A 2 = 650   m m 2 = 0,00065   M 2 ;

V 2 = V 1 A 1 A 2 = 3 ⋅ 0,0025 0,00065 = 11,54   m / s ;

P 1 = 103   k P a ;

ρ = 1000   k g / m 3 .

Temos:

R x = - 103 x 10 3 ⋅ 0,0025 - 1000 ⋅ 3 2 ⋅ 0,0025 + 11,54 2 ⋅ 0,00065

R x = - 366,6   N

Resposta

R x = - 366,6   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em determinado local, um helicóptero exige mais energia no verão ou no inverno para atingir um desempenho especificado? Explique.
Para flutuar no alto de uma montanha, um helicóptero precisa de mais, menos ou da mesma potência que precisaria para flutuar no nível do mar? Explique.
Um jato d’água horizontal de um bocal com seção transversal de saída constante atinge normalmente uma placa plana vertical e fixa. Determinada força F é necessária para manter a placa contra a corrent
Descreva por que um helicóptero flutua no ar em termos do momento e do escoamento de ar.
Um jato d’água horizontal com 5c m de diâmetro e velocidade de 30m / s atinge uma placa plana fixa vertical. A água se espalha em todas as direções no plano da placa. Qual a força necessária para mant