Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 42
Um tanque retangular, usado para fornecer água em uma experiência de número de Reynolds, tem profundidade de , largura e comprimento . O número de Reynolds da água do tubo de saída (diâmetro interno ) é , quando o tanque está metade cheio. A válvula de admissão de água para o tanque está fechada. Determine a taxa de variação do nível da água nesse instante.
Passo 1
Primeiro, temos que encontrar as propriedades da água na temperatura de . Temos que a viscosidade cinemática da água a é .
A equação para o número de Reynolds é:
Podemos reescrever explicitando a velocidade:
Aqui, o número de Reynolds é , o diâmetro interno é e a velocidade é . Com os valores fornecidos no enunciado, podemos encontra a velocidade substituindo na equação.
Passo 2
Podemos fazer um diagrama esquemático do volume de controle da seguinte maneira:
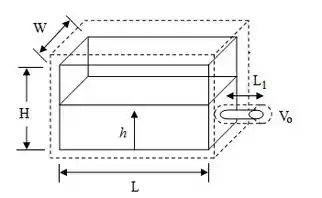
Onde a parte pontilhada representa o volume de controle.
Passo 3
Podemos aplicar a equação da conservação de massa para o volume de controle. Usando a equação básica, temos:
Temos que é o volume total do volume de controle ou seja, . Temos também que é a área total da superfície de controle, ou seja . Assim, a resolução da integral fica:
Como a densidade é constante, ela pode ser retirada da equação.
Passo 4
Resolvemos agora a derivada parcial.
Como o comprimento é constante, sua derivada é zero.
Passo 5
Para encontrar a taxa de variação do nível da água, basta substituir os dados fornecidos no enunciado na equação encontrado no passo 4. Assim temos:
Substituindo:
Portanto, a taxa de alteração do nível da água no tanque é .