Água pressurizadaentra na base de um longo tubo vertical, com comprimento e diâmetro, a uma vazão mássica de. O tubo está localizado no interior de uma câmara de combustão, o que resulta em transferência de calor para o tubo. Vapor d’água superaquecido sai no topo do tubo a e. Determine a mudança nas taxas nas quais as grandezas a seguir entram e saem do tubo: (a) a energia térmica combinada com o trabalho de fluxo; (b) a energia mecânica; (c) a energia total da água. Também, (d) determine a taxa de transferência de calor através da parede do tubo, . Sugestão: Propriedades relevantes podem ser obtidas em textos de termodinâmica.
Passo 1
Essa questão é sobre um tubo vertical beeem longo e fino em que passa uma corrente de água pressurizada. Ilustrando a situação, temos:
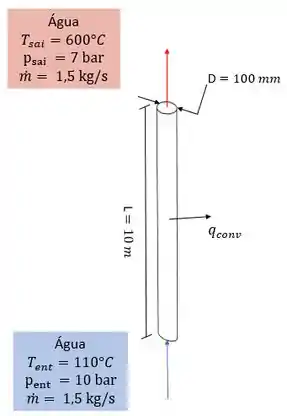
Dadas essas informações, precisamos calcular a energia térmica que entra e sai dos tubos, a energia mecânica, a energia total da água e a taxa de transferência de calor através da parede do tubo, .
Passo 2
Para resolver essa questão, vamos considerar que a vazão da água é constante e estamos em condição de estado estacionário, por isso que .
Então, vamos começar pela (a) em que queremos a energia térmica de entrada e saída do tubo. Para isso, vamos utilizar a equação da energia combinada com o trabalho de flux:
Primeiro precisamos calcular o volume, que vai ser:
Substituindo os valores para encontrar a energia de entrada (lembrando de colocar a unidade da pressão em SI), temos:
Analogamente, temos que a energia de saída é:
Passo 3
Resolvendo agora a letra (b), queremos calcular a energia mecânica, para isso vamos usar a equação:
Substituindo os valores que temos e pegando o valor de da água em textos termodinâmicos, como indica o enunciado, temos:
Passo 4
Na letra (c) queremos saber qual é a energia total da água. Para isso, vamos utilizar a seguinte equação:
Substituindo os valores que já calculamos na (a) e na (b), temos:
Passo 5
E por últimos, vamos resolver a letra (d), em que queremos a taxa de transferência de calor através da parede do tubo. Mas,
Então,
Resposta
- e