Um conjunto de instrumentos tem uma superfície externa esférica de diâmetro e emissividade. O conjunto é colocado no interior de uma grande câmara de simulação espacial cujas paredes são mantidas a. Se a operação dos componentes eletrônicos se restringe à faixa de temperaturas de, qual é a faixa aceitável de dissipação de potência do conjunto de instrumentos? Apresente os seus resultados graficamente, mostrando também o efeito de variações na emissividade ao considerar os valores dee .

Para resolver essa questão, vamos considerar que:

1. Estamos em condição de estado estacionário;
2. A temperatura da superfície é uniforme;
3. As paredes da câmara são grandes em comparação com o conjunto esférico.

A partir de um balanço geral de energia no conjunto esférico, a dissipação de energia interna será transferida por troca de radiação entre o conjunto e as paredes da câmara. De acordo com a equação de calor por radiação, temos:

Para a condição em que, com a área superficial sendo,

A dissipação de potência será:

Por último, precisamos fazer o gráfico que a questão nos pede. Repetindo o cálculo anterior para a faixa de , podemos obter a dissipação de potência em função da temperatura da superfície para a condição. Da mesma forma, com e , a família de curvas obtida é:

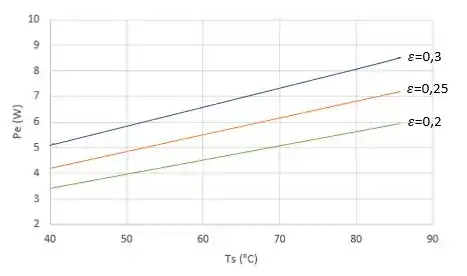
Assim, vemos que, como esperado, a dissipação de potência aumenta com o aumento da emissividade e da temperatura da superfície.