Um procedimento comum para medir a velocidade de correntes de ar envolve a inserção de um fio aquecido eletricamente (chamado de anemômetro de fio quente) no escoamento do ar, com o eixo do fio orientado perpendicularmente à direção do escoamento. Considera-se que a energia elétrica dissipada no fio seja transferida para o ar por convecção forçada. Consequentemente, para uma potência elétrica especificada, a temperatura do fio depende do coeficiente de convecção, o qual, por sua vez, depende da velocidade do ar. Considere um fio com comprimento e diâmetro , para o qual foi determinada uma calibração na forma . A velocidade e o coeficiente de convecção têm unidades de e , respectivamente. Em uma aplicação envolvendo ar a uma temperatura, a temperatura superficial do anemômetro é mantida a , com uma diferença de voltagem de e uma corrente elétrica de . Qual é a velocidade do ar?
Passo 1
Nessa questão nós temos o comprimento, diâmetro e calibração de um anemômetro de fio aquecido. Além da temperatura do escoamento de ar, a corrente e queda de tensão do anemômetro e temperatura da superfície do fio para uma aplicação específica. Ilustrando isso, temos:
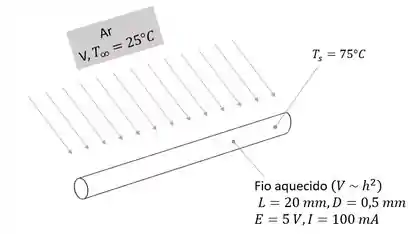
E com esses dados, a questão nos pede para calcular a velocidade do ar que está em função do coeficiente de convecção. Então partiu calcular !
Passo 2
Vamos assumir que estamos na condição de estado estacionário e que a transferência de calor do fio por convecção natural ou radiação é desprezível. A partir disso nós vamos analisar que se toda a energia elétrica for transferida por convecção ao ar, a seguinte igualdade deverá ser satisfeita:
Sendo que nós já vimos na Física que , então:
Onde é a área superficial do cilindro, então,
Isolando o que é o que queremos no momento ficamos com:
Passo 3
Agora que já temos a expressão do coeficiente de convecção, podemos substituir os valores:
E com encontramos a velocidade do ar a partir da expressão que o enunciado nos deu.
Com isso, vemos que o coeficiente de convecção é suficientemente grande para tornar insignificantes os efeitos da convecção natural e radiação.