Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas Abrangentes - Ex. 5

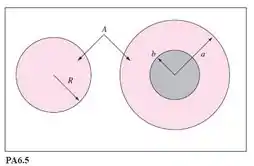
Água a temperatura ambiente escoa à mesma vazão volumétrica, Q = 9,4 × 10 - 4   m 3 / s , por dois tubos, um de seção circular e outro de seção anular. A área da seção transversal A dos dois tubos é idêntica, e todas as paredes são feitas de aço comercial. Ambos os tubos têm o mesmo comprimento. Nas seções transversais mostradas na Figura PA6.5, R = 15,0   m m e a = 25,0   m m . (a) Qual é o raio b de tal modo que as áreas das seções transversais dos dois tubos sejam idênticas? (b) Compare a perda de carga por atrito, h p d , por unidade de comprimento do tubo para os dois casos, considerando escoamento totalmente desenvolvido. Para a área anular, faça um cálculo rápido (usando diâmetro hidráulico) e um cálculo mais preciso (usando a correção do diâmetro efetivo), comparando ambos. (c) Se as perdas forem diferentes para os dois casos, explique por quê. Qual tubo é mais “eficiente”?

Passo 1

E simbora lá!

Já que as áreas são iguais, teremos:

A = π R 2 = π ( a 2 - b 2 )

Ou,

b = a 2 - R 2 = 25   m m 2 - 15   m m 2 = 20   m m

Dale, já temos (a).

Passo 2

Tendo para a água ν = 1,005 E - 6   m 2 / s , assim:

V = Q A = 9,4 × 10 - 4 m 3 s π 0,015   m 2 = 1,33   m / s

Logo,

R e = V D ν = 1,33 m s 0,03   m 1,005 E - 6 m 2 s = 39700

ϵ d 0,00153 → f m o o d y = 0,0261

Calculando a perda de carga:

h f L = f D V 2 2 g = 0,0261 0,03 1,33 2 2 9,81 = 0,0785  

Para o anular, teremos D h = 4 A P = 2 a - b = 20   m m , e a mesma velocidade de 1,33 m/s, assim:

R e D h = V D h ν = 26500

ϵ D h = 0,0023 → f m o o d y = 0,0291

Assim, a perda de carga

h f L ≈ f D h V 2 2 g = 0,131

Por diâmetro efetivo, teremos b/a=0,8, pela Tabela 6.3, teremos D e f e t i v o = 0,667 D h = 13,3   m m , logo:

R e D e f e t i v o = 17700

ϵ D e f e t i v o = 0,00345 → f m o o d y = 0,0327

Assim, a perda de carga:

h f L = f D h V 2 2 g = 0,147

Passo 3

Temos no tubo anular uma maior perda de carga, assim, o mais efetivo seria o tubo de seção circular.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deseja-se fornecer 60m 3 / h de água a 20°C por um tubo horizontal de ferro fundido asfaltado. Calcule o diâmetro do tubo que causará uma queda de pressão de exatamente 40 kPa por 100 m de comprimento
Repita o Problema 6.26 usando água a 20°C como fluido. É um pouco mais trabalhoso que o problema original, mas os conceitos básicos são exatamente os mesmos. Outra vez, despreze as perdas localizadas.
Para o sistema da Figura P6.55, admita Δ z = 80m e L = 185m de tubo de ferro fundido. Para qual diâmetro do tubo a vazão será de 7 m 3 / h ?
Se dois tubos na figura abaixo são colocados em série com a mesma queda total de pressão de 20,7 kPa, qual será a vazão? O fluido é óleo SAE 10 a 20°.
Para o escoamento de água, com um número de Reynolds de 1,03x10 6 , por um tubo de 5 cm de diâmetro e altura da rugosidade de 0,5 mm, o fator de atrito de Moody é aproximadamente:0,0120,0180,0380,0490