Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 159

Aletas anulares de alumínio com perfil retangular estão fixadas a um tubo circular que possui diâmetro externo de 50   m m e uma temperatura na superfície externa igual a 200 ° C . As aletas possuem 4   m m de espessura e 15   m m de comprimento. O sistema se encontra no ar ambiente a 20 ° C , com um coeficiente convectivo na superfície de 40   W / ( m 2   ·   K ) .

(a) Quais são a eficiência e a efetividade das aletas?

(b) Se existirem 125 dessas aletas por metro de comprimento do tubo, qual é a taxa de transferência de calor por unidade de comprimento do tubo?

Passo 1

Aqui nós temos as dimensões e temperatura da base de aletas de alumínio de perfil retangular. Além das condições do ar ambiente. Esquematicamente:

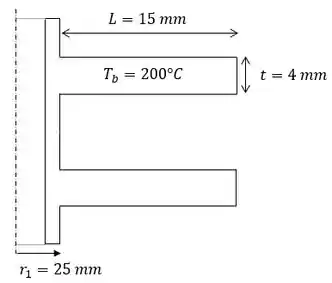
A partir desse sistema queremos calcular a eficiência e efetividade da aleta e a taxa de transferência de calor por unidade de comprimento do tubo. Então vamos lá!

Passo 2

Para resolver essa questão vamos assumir que:

(1) Estamos em condição de estado estacionário;

(2) A condução radial é unidimensional nas aletas;

(3) As propriedades são constantes;

(4) A radiação e resistência de contato são desprezíveis;

(5) O coeficiente de convecção é uniforme.

Na letra (a) queremos calcular a eficiência e a efetividade das aletas, onde os parâmetros da aleta podem ser calculados da seguinte forma:

r 2 c = r 2 + t 2 = 40 m m + 2 m m = 0,0 42 m

r 2 c r 1 = 0,042 m 0,025 m = 1 , 68

L c = L = t 2 = 15 m m + 2 m m = 0,01 7 m

A p = L c t = 0,0 17 m × 0,00 4 m = 6,8 × 10 - 5 m 2

L c 3 2 h k A p 1 2 = 0,01 7 m 3 2 40   W / ( m 2   ·   K ) 240 W m   ·   K × 6,8 × 10 - 5 m 2 1 2 = 0,1 1

Onde o valor de k foi retirado da Tabela A.1 para o alumínio puro à T ≈ 400 K .

Passo 3

Então, a eficiência da aleta é η f   ≈   0,97 e a taxa de calor da aleta é:

q f = η f q m a x = η f h A f a n n θ b = 2 π η f h ( r 2 , c 2 - r 1 2 ) θ b

q f = 2 π × 0,97 × 40 W m 2   ·   K × 0,042 m 2 - 0,025 m 2 180 ° C

q f = 50   W

E a efetividade da aleta é:

ε f = q f h A c , b θ b = 50 W 40 W m 2   ·   K × 2 π 0,025 m 0,004 m 180 ° C

ε f = 11,05

Passo 4

Já na letra (b) queremos a taxa de transferência de calor por unidade de comprimento do tubo para 125 aletas.

q ' = N ' q f + h 1 - N ' t 2 π r 1 θ b

q ' = 125 × 50 W / m + 40 W m 2   ·   K 1 - 125 × 0,00 4 m × 2 π × 0,0 25 m 180 ° C

q ' = 6250   + 565 W m = 6,82 k W / m

Resposta

  1. η f   ≈   0,97 e ε f = 11,05
  2. q ' = 6,82 k W / m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas aletas do tipo pino são idênticas, exceto que o diâmetro de uma delas é duas vezes o diâmetro da outra. Para qual aleta a (a) eficácia e (b) eficiência da aleta é maior? Explique.
Duas superfícies aletadas são idênticas, exceto que o coeficiente de transferência de calor por convecção de uma delas é duas vezes superior ao da outra. Para qual superfície da aleta a (a) eficácia d
Como a eficácia global de uma superfície aletada difere da eficácia de uma única aleta?
A (a) eficiência e (b) a eficácia das aletas aumentam ou diminuem se seu comprimento aumentar?
Considere uma aleta retangular muito longa fixada a superfície plana, de tal forma que a temperatura na sua ponta seja essencialmente a mesma do ar circundante, ou seja, 20°C. Sua largura é de 5,0 cm;