Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas Abrangentes - Ex. 1
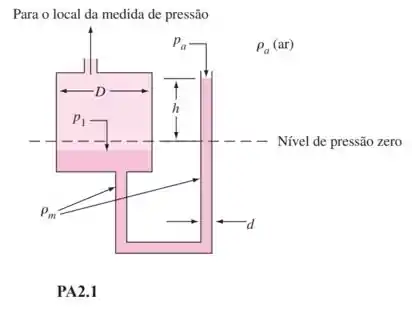
Alguns manômetros são construídos como na Figura PA2.1, em que um lado é um grande reservatório (diâmetro ) e o outro lado é um pequeno tubo de diâmetro , aberto para a atmosfera. Em um caso assim, a altura do líquido manométrico no lado do reservatório não muda apreciavelmente. Isso tem a vantagem de que somente uma altura precisa ser medida, não duas. O líquido manométrico tem massa específica , enquanto o ar tem massa específica . Ignore os efeitos da tensão superficial. Quando não há diferença de pressão no manômetro, as elevações em ambos os lados são as mesmas, o que é indicado pela linha tracejada. A altura é medida com base no nível de pressão zero, como mostra a figura.
- Quando é aplicada uma alta pressão ao lado esquerdo, o líquido manométrico do reservatório desce, enquanto o líquido no tubo sobe para conservar a massa. Escreva uma equação exata para , levando em conta o movimento da superfície do reservatório. A sua equação deverá fornecer em função de e os parâmetros físicos o problema, e a constante da gravidade
- Escreva uma expressão aproximada para , desprezando a alteração na elevação da superfície do reservatório de líquido.
- Considere em uma certa aplicação. Se e o líquido manométrico tiver uma massa específica de , calcule a razão requerida para manter o erro da aproximação da parte (b) dentro de da medida exata da parte . Repita para um erro dentro de .
Passo 1
Ufa! Terminou de ler o enunciado aí?? Ahahaaha
Enfim, parece questão de Enem mas não. Mas vamos juntos.
Bom, você já deve ter se acostumado a ver esses tubo e pensar “a pressão aqui é igual aqui e é isso”. Certo?
E é isso mesmo, tudo que o exercício quer é a pressão ali, que deve ser igual a pressão no tubo menor. Para tanto vamos chamar a altura de até a linha tracejada (nível de pressão zero) de .
Ok então, podemos chegar no seguinte:
Tá comigo?!
Mas pouxa vida, o exercício não quer esse na resposta, então precisamos lembrar que o volume de líquido deslocado, ou seja, aquele volume que desce uma altura no reservatório deve ser igual ao volume que sobe no tubo menor. Portanto:
Simples, não?
Passo 2
Devolvendo isso na nossa equação:
Mas o exercício quer né?! Isso! Então a pressão manométrica será a pressão no ponto menos a pressão atmosférica:
Show de bola! Essa foi a nossa imensa alternativa (a).
Já a alternativa (b) ele quer que a gente desconsidere aquele . Fica muito mais fácil então:
Tá tranquilo por enquanto né?!
Mas pense bem, no porquê do exercício mandar a gente desconsiderar esse ... Ele faz isso pq na letra (a) temos uma expressão exata para enquanto que na (b) a gente faz uma aproximação, desconsiderando essa variação no reservatório. Naturalmente, quanto maior o revervatório, menos variação teremos nessa altura, até que ela se torna desprezível.
Passo 3
A ideia agora na alternativa (c) é justamente ver quanto essa aproximação é boa. Pra isso a gente só precisa dos diâmetros desses caras, e jogar na fórmula do Erro:
Mas em vez de calcular esses valores, você pode só fazer uma brincadeira com as fórmulas já encontradas:
Naturalmente, podemos cancelar tudo aquilo que é comum:
Se você brincar um pouquinho com essa fórmula, podemos chegar na relação pedida:
Então, a razão requerida para manter o será:
E para um erro de :
Um bocado assuatador, mas bem tranquilo né?! Até a próxima!
Resposta
Portanto:
- para e para