Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 46

Uma porta de acesso, de 1   m de largura e 1,5   m de altura, está localizada em uma parede plana e vertical de um tanque de água. A porta é articulada ao longo da sua borda superior, que está 1   m abaixo da superfície da água. A pressão atmosférica atua na superfície externa da porta. ( a ) Determine o módulo e a linha de ação da força resultante de todos os fluidos agindo sobre a porta. ( b ) se a pressão manométrica na superfície da água for aumentada para 0,3   a t m , qual será a resultante da força e a sua linha de ação? ( c ) Trace os gráficos da razão F / F 0 e y ’ / y c para valores diferentes da razão de pressões superficiais p s / p a t m . ( F 0 é a força resultante quando p s   =   p a t m .)

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema vai ser dividido em duas partes. Na primeira, temos que encontrar a resultante da linha de ação pela pressão atmosférica e na segunda, para p s g = 0,3   atm. Com isso, vamos aplicar as equações hidrostáticas para esse sistema. Logo, vamos obter uma expressão geral para a força e a linha de ação. Temos:

F R = ∫ p   d A = ∫ c c + a p b   d y F R = ∫ c c + a p s g + ρ g y b   d y = b p s g a + ρ g 2 a 2 + 2 a c   ( a )

y ' F R = ∫ y p   d A y ' = b F R p s g 2 c + a 2 - c 2 + ρ g 3 c + a 3 - c 3  

Simplificando:

y ' = b F R p s g 2 a 2 + 2 a c + ρ g 3 a 3 + 3 a c ( a + c )   ( b )

Onde ( a ) é um fluido estático e ( b ) , um fluído incompressível. Para a primeira parte do problema, temos p s g = 0 e, substituindo em ( a ) , temos:

F o = ρ g b 2 a 2 + 2 a c

Substituindo:

F o = 1 2 ∙ 999 k g m 3 × 9,81 m s 2 × 1   m 1,5   m 2 + 2 × 1,5   m × 1 m N s 2 k g   m   F o = 25,7   k N

Para a parte ( b ) , para a linha de ação, temos:

y ' = ρ g b 3 F o a 3 + 3 a c a + c

Substituindo:

y ' = 1 3 ∙ 999 k g m 3 × 9,81 m s 2 × 1   m × 1 27,7 × 10 3 1 N   1,5   m 3 + 3 × 1,5   m × 1 m 1,5   m + 1   m N s 2 k g   m

y ' = 1,9   m

Passo 2

Agora, para a segunda parte, onde p s g = 0,3   a t m , temos para ( a ) :

F R = 1   m 0,3   a t m × 1,013 × 10 5   N m 2   a t m   × 1,5   m + 1 2 × 999 k g m 3 × 9,81 m s 2 1,5   m 2 + 2 × 1,5   m × 1 m N s 2 k g   m   F R = 71,3   k N

Para, ( b ) , Substituindo em ( 2 ) , temos:

y ' = 1   m 0,3   a t m × 1,013 × 10 5   N m 2   a t m   × 1,5   m + 1 2 × 999 k g m 3 × 9,81 m s 2 1,5   m 2 + 2 × 1,5   m × 1 m N s 2 k g   m   71,3 × 10 3 y ' = 1,789   m

Logo:

F F o = b [ p s g a + ρ g 2 ( a 2 + 2 a c ) ] ρ g b 2 ( a 2 + 2 a c ) = 1 + 2 p s g ρ g a + 2 c

Já para o portão, onde y c = c + a / 2 . Temos:

y ' y c = 2 b F R 2 c + a p s g 2 a 2 + 2 a c + ρ g 3 a 3 + 3 a c a + c   = 2 b ( 2 c + a ) × p s g 2 a 2 + 2 a c + ρ g 3 a 3 + 3 a c a + c b p s g a + ρ g 2 a 2 + 2 a c  

Simplificando:

y ' y c = 2 ( 2 c + a ) × p s g 2 a 2 + 2 a c + ρ g 3 a 3 + 3 a c a + c p s g a + ρ g 2 a 2 + 2 a c

Passo 3

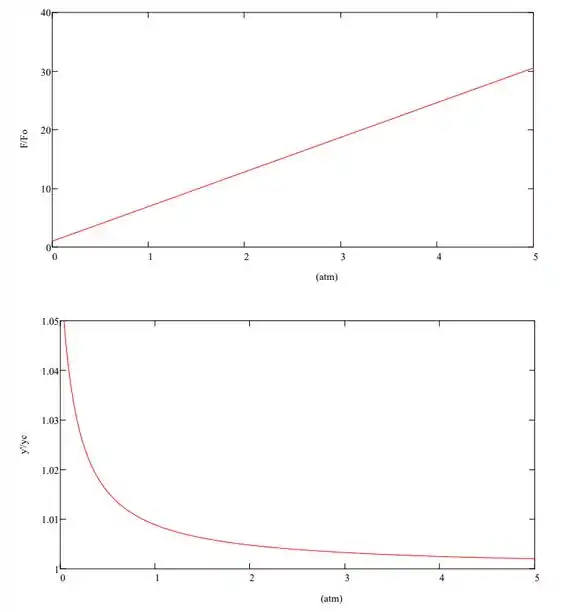
Por fim, com base nessas expressões, vemos que a força na porta varia linearmente com o aumento da pressão superficial e que a linha de a ação da resultante está sempre abaixo do centróide do porta. Também podemos concluir que à medida que a pressão aumenta, no entanto, a linha de ação se aproxima do centróide. Sendo assim, o esboço dos nossos gráficos fica assim:

Resposta

F o = 25,7   k N

y ' = 1,9   m

F R = 71,3   k N

y ' = 1,789   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura FE2.3, se o óleo da região B tem d = 0,8 e a pressão absoluta no ponto A é 1a t m , qual é a pressão absoluta no ponto B ? 5,6k P a 10,9k P a 107k P a 112k P a 157k P a
Um manômetro ligado a um tanque de nitrogênio pressurizado registra uma pressão manométrica de 711m m de mercúrio. Se a pressão atmosférica for de 101,3k P a , qual é a pressão absoluta no tanque? 95k
Em um dia normal ao nível do mar, um manômetro, colocado abaixo da superfície do oceano ( d = 1,025 ) , registra uma pressão absoluta de 1,4M P a . A que profundidade se encontra o instrumento? 4m 129
Na figura FE2.3, se o óleo na região B tem d = 0,8 e a pressão absoluta no ponto B é 96,5 k P a , qual é a pressão absoluta no ponto A?
Um malandro colocou óleo, de densidade d o , no ramo esquerdo do manômetro da Figura PQ2.2. Não obstante, o tubo em U ainda é útil como um dispositivo de medida de pressão. Ele é ligado a um reservató