Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 16
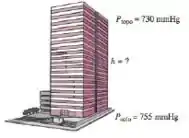
O barômetro básico pode ser usado para medir a altura de um prédio. Se as leituras barométricas nas partes superior e inferior de um prédio são de e , respectivamente, determine a altura do prédio. Considere a densidade média do ar de .
Passo 1
Bom galera, nesse problema temos um barômetro sendo usado para medir a altura de um edifício, registrando a leitura na parte inferior e na parte superior da
o edifício. Assim, devemos encontrar a altura do prédio
Vamos considerar que a variação da densidade do ar com a altitude é insignificante.
Passo 2
Começando, vamos calcular as pressões atmosféricas na parte superior e inferior do edifício:
Agora, para a parte inferior:
Escrevendo um equilíbrio de força por unidade de área base, temos:
Assim,
Prontinho!!
Resposta
Exercícios de Livros Relacionados
No manômetro da figura, o fluido A é a água e o fluido B , mercúrio. Qual é a pressão p 1 ? Dados: γ H g = 136000N / m 2 ; γ H 2 O = 10000N / m 2 .
Determinar ρ A , p 0 e p 0 , a b s na configuração do desenho, sendo dados: h B = 0,1m ; h A = 0,2m ; ρ B = 1000k g / m 3 ; p a t m = 100k P a ; g = 10m / s 2 .
Determinar as pressões efetivas e absolutas:Do ar;No ponto M , na configuração a seguir.Dados: leitura barométrica 740m m H g ; γ ó l e o = 8500N / m 3 ó ; γ H g = 136000N / m 3 .
Calcular a leitura do manômetro A da figura. γ H g = 136.000N / m 3
No manômetro diferencial da figura, o fluido A é água, B é óleo e o fluido manométrico é mercúrio. Sendo h 1 = 25c m , h 2 = 100c m , h 3 = 80c m e h 4 = 10c m , qual é a diferença de pressão p A - p