Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 80

Uma barragem cilíndrica tem diâmetro de 3 m e comprimento de 6 m. Determine o módulo e o sentido da força resultante da água agindo sobre a barragem.

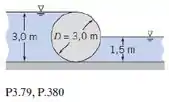
Passo 1

Nessa questão temos um açude cilíndrico e devemos encontrar a magnitude e direção da força resultante da água no açude.

Agora vamos ver com quais expressões podemos calcular isso:

d p d h = ρ g , pressão hidrostática onde h é positivo para baixo.

d F R → = - p d A → , força hidrostática

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando em superfícies livres e no primeiro quadrante do cilindro.

Passo 2

Para resolvermos, temos o seguinte diagrama:

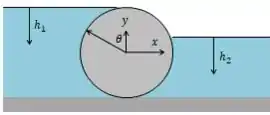
Agora vamos usar um sistema de coordenadas:

F R x = F R i ^ = - ∫ p d A → i ^ = - ∫ p cos ⁡ θ + 90 ° d A = ∫ p sin ⁡ θ d A

Para o eixo y :

F R y = F R j ^ = - ∫ p d A → j ^ = - ∫ p cos ⁡ θ d A

Como d A = L R   d θ , substituindo, temos:

F R x = ∫ 0 3 2 π p L R sin ⁡ θ d A                       F R y = - ∫ 0 3 2 π p L R cos ⁡ θ d A

Agora sim podemos aplicar a integração, masss, acima da faixa 0   ≤   θ   ≤   π , temos h 1 = R ( 1 - cos ⁡ θ ) . Já no intervalo π ≤ θ ≤ 3 2 π , temos h 2 = - R cos ⁡ θ .

Passo 3

Agora, vamos expressar a pressão em termos de θ e substituir nas equações de força:

F R x = ∫ 0 3 2 π p L R sin ⁡ θ d θ

F R x = ∫ 0 π ρ g R ( 1 - cos ⁡ θ ) L R sin ⁡ θ   d θ - ∫ π 3 2 π ρ g R cos ⁡ θ L R sin ⁡ θ d θ

F R x = ρ g R 2 L ∫ 0 π 1 - cos ⁡ θ sin ⁡ θ   d θ - ∫ π 3 2 π cos ⁡ θ sin ⁡ θ d θ

Resolvendo...

F R x = ρ g R 2 L 2 - 1 2 = 3 2 ρ g R 2 L

Substituindo valores:

F R x = 3 2 × 999 k g m 3 × 9,81 m s 2 × ( 1,5   m ) 2 × 6 m = 198,5   k N

Passo 4

Fazemos o mesmo procedimento para achar a componente y :

F R y = - ∫ 0 3 2 π p L R cos ⁡ θ d θ

F R y = - ∫ 0 3 2 π ρ g R 1 - cos ⁡ θ L R cos ⁡ θ d θ - ∫ π 3 2 π ρ g R cos ⁡ θ L R cos ⁡ θ d θ

F R y = - ρ g R 2 L ∫ 0 π 1 - cos ⁡ θ cos ⁡ θ d θ - ∫ π 3 2 π cos ⁡ θ 2 d θ

F R y = ρ g R 2 L π 2 + 3 π 4 - π 2 = 3 π 4 ρ g R 2 L

Substituindo valores:

F R y = 3 π 4 × 999 k g m 3 × 9,81 m s 2 × 1,5 2 × 6 m = 312   k N

Agora é só calcular a força resultante:

F R = 312 × 10 3 N 2 + 198,5 × 10 3   N 2

F R = 370   k N

Prontinho!!

Resposta

F R = 370   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma janela de acesso, na forma de um triângulo isósceles e articulada no topo, é colocada na parede vertical de uma forma contendo concreto líquido. Determine a força mínima que deve ser aplicada no p
Resolva novamente o Exemplo 3.6, usando o método das duas pressões separadas. Considere a força distribuída como a soma de uma força F 1 causada pela pressão manométrica uniforme com uma força F 2 cau
Um grande tanque aberto contém água e está conectado a um condutor com 2m de diâmetro conforme mostrado. Um tampo circular é usado para selar o condutor. Determine o modulo, o sentido e a localização
As comportas de Poe Lock, no Salto de Santa Maria em Michigan, fecham um canal com largura W = 34 m, comprimento L = 360 m e profundidade D = 10 m. A geometria de um par de comportas é mostrada na fig
O que sustenta um carro sobre seus pneus? A maioria das pessoas pensa que é a pressão do ar dentro dos pneus. Contudo, a pressão interna é a mesma em volta do pneu. Assim, a pressão de ar que empurra