Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 56
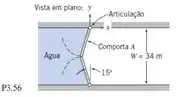
As comportas de Poe Lock, no Salto de Santa Maria em Michigan, fecham um canal com largura W = 34 m, comprimento L = 360 m e profundidade D = 10 m. A geometria de um par de comportas é mostrada na figura; cada comporta é articulada na junção com a parede do canal. Quando fechadas, as bordas das comportas são forçadas no centro, uma contra a outra, pela água. Avalie a força exercida pela água sobre a comporta A. Determine o módulo e o sentido das componentes da força exercida pela comporta sobre a articulação. (Despreze o peso da comporta.)
Passo 1
Bom, pra começo de conversa o que temos a resolver é um problema de sistema das comportas. Como todo exercício de estática dos fluidos, consideramos aqui que a densidade é constante.
Analisamos as forças existentes no eixo e , podemos perceber que há varias forças agindo, como mostra a figura:
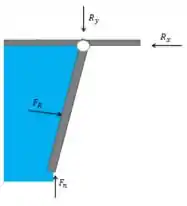
Então unimos essas forças num somatório, né não? hehe. Sabendo que a força relativa ao problema é a pressão, temos então:
Integrando essa equação, fica:
Temos também outra equação da estática que é:
E, por último, a que é retirada da equação de Bernoulli:
Pronto! Podemos dizer que cada portão é igual a um retângulo, onde a profundidade é , chamaremos então de . Para a largura temos que considerar o ângulo submetido, logo
Passo 2
Fazemos as relações agora. será a força resultante em relação ao eixo (altura), logo
Mas o diferencial de área é dado por: . O intervalo de integral é de a . Portanto,
Resolvendo a integral temos:
Agora é só substituir os dados para achar a força resultante.
Passo 3
Para determinar o módulo e o sentido dos componentes, visualizamos para onde aponta a seta para saber o sinal positivo ou negativo. A falta de atenção nesse quesito pode comprometer toda a resposta!
Calculando pela força da dobradiça, temos:
Agora calculamos ,
E, por fim,
Resposta
e