Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 58

Uma janela de acesso, na forma de um triângulo isósceles e articulada no topo, é colocada na parede vertical de uma forma contendo concreto líquido. Determine a força mínima que deve ser aplicada no ponto D para manter a janela fechada, considerando a configuração da forma e do concreto conforme mostrado. Plote os resultados para a faixa de profundidade do concreto de 0   ≤   c   ≤   a .

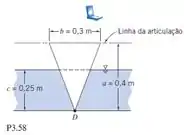
Passo 1

Bom, a janela possui suas dimensões exatas. É necessário que apliquemos as equações hidrostáticas no sistema, sendo elas:

d p d h = ρ g

F R = ∫ p d A

y ' × F R = ∫ y p d A  

∑ M = 0 , equilíbrio rotacional

Assim, a nossa missão é encontrar a força mínima aplicada em D necessária para manter a janela fechada e plotar os resultados na faixa de profundidade do concreto entre 0 e a .

Fazemos algumas considerações: fluido estático; fluido incompressível; a pressão atmosférica atua na superfície livre e fora da janela.

O diagrama que representa esse sistema é o seguinte:

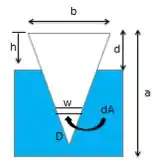
Passo 2

O primeiro passo para as contas é a integração da equação de pressão. Portanto, a partir do diagrama podemos estabelecer que para h > d , temos p   =   ρ g ( h   -   d ) e para h < d , p = 0 , sendo que d = a - c = 0,15   m .

Relacionando os momentos da dobradiça, temos

F D × a + ∫ h p d A = 0  

Logo, F D é dado por

F D = 1 a ∫ h p d A

Como o intervalo é de a até d e substituindo a área:

F D = 1 a ∫ d a h ρ g ( h   -   d ) w d h

Podemos calcular w por semelhgança de triângulos, ou seja

w b = a - h a               ∴         w = b ( a - h ) a

Substituindo na equação de F D fica:

F D = ρ g a ∫ d a b a h ( h   -   d ) ( a - h ) d h

F D = ρ g b a 2 ∫ d a - h 3 + a + d h 2 - a × d × h d h

Calculando a integral, temos

F D = ρ g b a 2 - a 4 - h 4 4 + a + d a 3 - d 3 3 - a   d   a 2 - d 2 2

Organizando os termos:

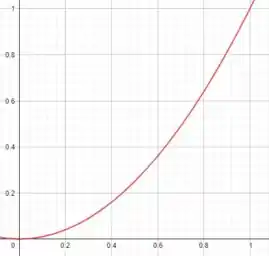
F D = ρ g b a 2 - 1 4 1 - d a 4 + 1 3 1 + d a 1 - d a 3 - 1 2 × d a 1 - d a 2

A partir dessa equação podemos plotar o gráfico. Para achar o valor de F D é só substituir os valores sendo: ρ = 2,5 × 10 3 k g / m 3 e d a = 0,375 . Com o uso de uma calculadora cientifica, obtemos o valor de F D = 32,9   N .

O gráfico ficará da seguinte forma:

Resposta

F D = 32,9   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque aberto está cheio com água na profundidade indicada. A pressão atmosférica atua sobre todas as superfícies externas do tanque. Determine o módulo e a linha de ação da componente vertical da
Um longo bloco de madeira, de seção quadrada, é articulado em uma de suas arestas. O bloco está em equilíbrio quando imerso em água na profundidade mostrada. Avalie a densidade relativa da madeira, se
Considere um recipiente semicilíndrico de raio R e comprimento L. Desenvolva expressões gerais para o módulo e a linha de ação da força hidrostática em uma extremidade, se o recipiente estiver parcial
Considere a barragem cilíndrica com diâmetro de 3 m e comprimento de 6 m. Se o fluido no lado esquerdo tem SG = 1,6 e o fluido no lado direito tem SG = 0,8, determine o módulo e o sentido da força res
Uma comporta Tainter, usada para controlar a vazão de água na represa de Uniontown no Rio Ohio, é mostrada na figura; a sua largura é w = 35 m. Determine o módulo, o sentido e a direção da linha de aç