Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 59
Resolva novamente o Exemplo 3.6, usando o método das duas pressões separadas. Considere a força distribuída como a soma de uma força causada pela pressão manométrica uniforme com uma força causada pelo líquido. Calcule essas forças e determine suas linhas de ação. Some, então, os momentos em relação à articulação para avaliar .
Passo 1
Retomando os dados do exemplo, temos as seguintes equações
Sendo o momento: . Agora, precisamos avaliar cada caso distribuindo as forças e , conforme a figura:
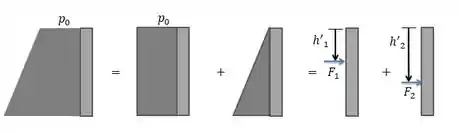
Para , no meio da porta, temos:
E a linha de ação é e .
E para , na ponta:
Como a porta é semelhante a um retângulo, o momento de área é:
Assim, podemos determinar as linhas de ação em relação a altura:
Passo 2
Como esse tipo de questão cobra um DCL (diagrama de corpo livre), então:
Assim, calculamos o momento de área em relação a :
Isolamos para calcular, temos então:
Assim, .