Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 153
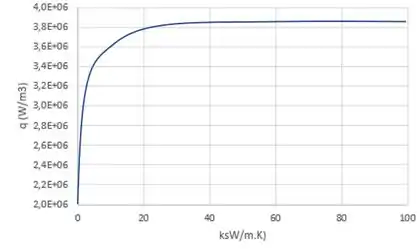
Em um bastão longo, com de diâmetro e condutividade térmica de há geração de energia térmica volumétrica uniforme de . O bastão é coberto com uma luva de isolante elétrico que possui de espessura e condutividade térmica de Uma estrutura com hastes retangulares, com as dimensões indicadas na figura, e condutividade térmica de é usada para sustentar o bastão e mantê-lo no centro de um tubo com de diâmetro. Ar a escoa sobre as superfícies das hastes com um coeficiente de transferência de calor igual a A superfície externa do tubo é isolada termicamente.
Desejamos aumentar o aquecimento volumétrico no interior do bastão, mas sem permitir que a temperatura no seu eixo central seja superior a . Determine o impacto das seguintes mudanças, que podem ser efetuadas independentemente ou em conjunto: (i) aumento da velocidade do ar e assim do coeficiente convectivo; (ii) mudança no número e/ou na espessura das hastes; e (iii) uso de uma luva não condutora elétrica com maior condutividade térmica (por exemplo, carbono amorfo ou quartzo). Recomende uma configuração realística que forneça um aumento significativo em
Passo 1
Aqui nós temos uma haste longa com geração volumétrica interna coberta por uma luva isolante eletricamente e apoiada por uma aranha nervurada. Onde o circuito térmico é:
E queremos encontrar uma combinação do coeficiente de convecção, design da aranha e condutividade térmica da luva, que aprimora o aquecimento volumétrico sujeito a uma temperatura máxima da linha central de .
Passo 2
Para resolver essa questão, vamos considerar que:
(1) Estamos em condição de estado estacionário;
(2) A transferência de calor radial é unidimensional na haste, luva e bastão;
(3) A resistências de contato interfacial é desprezível;
(4) As propriedades são constantes;
(5) A superfície externa é adiabática.
A taxa de aquecimento do sistema por unidade de comprimento pode ser expressa como:
Onde,
E,
A temperatura da linha central da haste está relacionada a da seguinte forma:
Passo 3
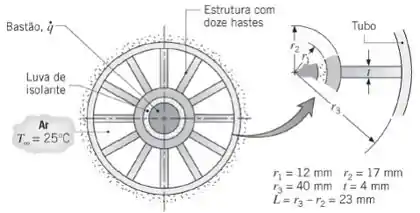
Para condições de caso base de e , , e . Como mostrado abaixo, pode ser aumentado aumentando , onde representa um limite superior razoável para o fluxo de ar. No entanto, um aumento de mais de vezes em produz apenas um aumento de em
A dificuldade é que, aumentando significativamente , a resistência térmica da matriz de aletas é reduzida para , tornando a luva o contribuinte dominante na resistência total.
Passo 4
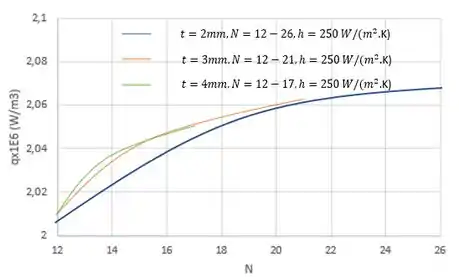
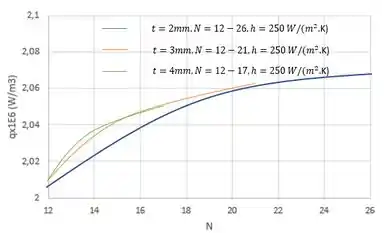
Resultados semelhantes ao anterior são obtidos quando e são variados. Para valores de e , foram consideradas variações de nas respectivas faixas e . O limite superior de foi fixado exigindo que para evitar uma resistência excessiva ao fluxo de ar entre as nervuras. Como mostrado abaixo, o efeito do aumento de é pequeno e há pouca diferença entre os resultados para os três valores de .
Passo 5
Em contraste, uma melhoria significativa está associada à alteração do material da luva e é necessário apenas (por exemplo, uma luva de boro) para se aproximar de um limite superior à influência de .
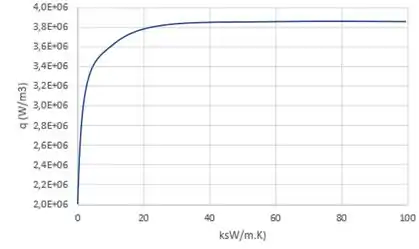
Para e , apenas uma ligeira melhora é obtida com o aumento de . Portanto, as condições recomendadas são:
Resposta
(i)
(ii)
(iii)
