Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 148
No Problema 3.146, o valor especificado para é alto e característico do resfriamento com líquidos. Na prática, seria preferível o uso de resfriamento com ar, no qual um limite superior razoável para o coeficiente convectivo seria Avalie o efeito de mudanças na geometria dos pinos na taxa de transferência de calor no chip se as demais condições do Problema 3.146, incluindo a temperatura máxima permissível para o chip de , permanecem válidas. Variações paramétricas que podem ser analisadas incluem o número total de pinos, , na matriz quadrada; o diâmetro do pino e o seu comprimento . No entanto, o produto não deve exceder a fim de garantir um escoamento adequado do ar através da matriz de pinos. Recomende um projeto que melhore o resfriamento do chip.
Passo 1
Essa questão está remetendo ao Problema 3.146 onde tínhamos a geometria da matriz de aletas de pinos usada como dissipador de calor para um chip de computador e as condições de convecção da matriz e substrato do chip. Onde o circuito térmico é representado por:
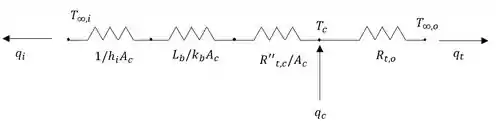
E nós queremos encontrar o efeito do diâmetro, espaçamento e comprimento do pino na dissipação máxima permitida de energia do chip. Então vamos para as nossas considerações!
Passo 2
Para resolver essa questão vamos assumir que:
(1) Estamos em condição de estado estacionário;
(2) A transferência de calor é unidimensional no conjunto de placas de aglomerado;
(3) A resistência de contato entre as aletas é desprezível;
(4) As propriedades são constantes;
(5) A resistência térmica é insignificante;
(6) A temperatura do chip é uniforme.
Com isso, nós temos que a dissipação total de energia é:
Onde,
E,
A resistência da matriz de pinos é:
Onde,
Passo 3
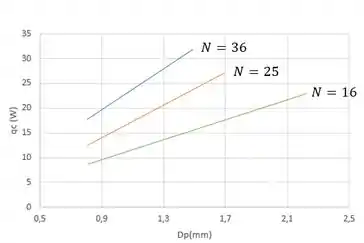
Sujeito à restrição de que , as expressões anteriores podem ser usadas para calcular em função de para e valores de e . Fazendo um gráfico, temos:
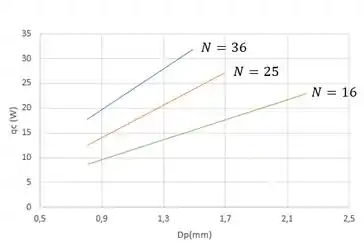
A partir do gráfico acima, vemos que é desejável maximizar o número de pinos e o diâmetro dos pinos, desde que as passagens de fluxo não sejam limitadas a ponto de exigir uma queda de pressão excessiva para manter o coeficiente de convecção prescrito. A taxa máxima de calor para o conjunto de aletas () corresponde a e . Melhorias adicionais podem ser obtidas usando pinos de diâmetro , que produzem .
Passo 4
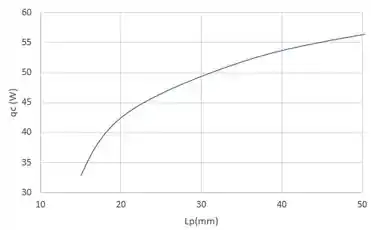
Explorando o efeito de para e , obtemos:
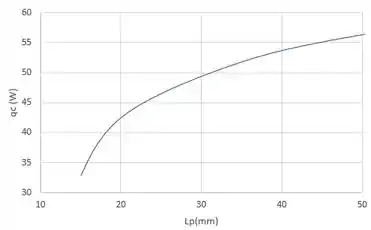
A partir do gráfico acima, vemos que há benefícios em aumentar a , embora o efeito diminua devido a uma redução resultante em (de para a para ). Embora seja obtida uma taxa de dissipação de calor de para , as restrições de volume do pacote podem impedir um comprimento de aleta tão grande.
Resposta
