Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 144
Um chip de silício isotérmico, com um lado de comprimento , encontra-se soldado a um dissipador de calor de alumínio com comprimento equivalente. O dissipador tem uma base com espessura e uma série de aletas retangulares, cada uma com comprimento . Um escoamento de ar com é mantido através dos canais formados pelas aletas e uma placa de cobertura, e para um coeficiente convectivo de é necessário um espaçamento mínimo entre as aletas de em função de limitações na queda de pressão no escoamento. A junta soldada tem resistência térmica de .
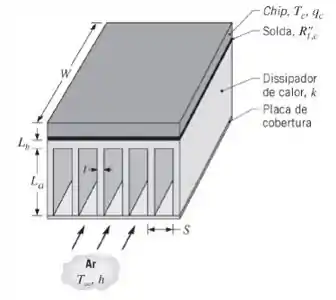
(a) Considere uma série que tem aletas, cujas limitações levam a valores da espessura da aleta de e do passo de , obtidos das imposições de que e . Se a máxima temperatura permitida do chip for , qual é o valor correspondente da potência do chip ? Uma condição de aleta com extremidade adiabática pode ser admitida e pode-se considerar que o escoamento do ar ao longo das superfícies externas do dissipador fornece um coeficiente convectivo equivalente ao associado ao escoamento do ar através dos canais.
(b) Com e fixos em e respectivamente, explore o efeito de aumentar a espessura das aletas através da redução do número de aletas. Com e fixo em , porém com a relaxação da limitação sobre a queda de pressão, explore o efeito de aumentar o escoamento do ar e assim o coeficiente convectivo.
Passo 1
Passo 1 Vamos para mais uma questão \o/. Aqui nós temos as dimensões e temperatura máxima permitida de um chip eletrônico. Assim como a resistência de contato térmico entre o chip e o dissipador de calor e as dimensões e condutividade térmica do dissipador de calor. Além do coeficiente de temperatura e convecção associado ao fluxo de ar através do dissipador de calor. Esquematicamente:
A partir disso, queremos calcular a potência máxima permitida do chip para o dissipador de calor, o efeito da espessura / número da aleta e o coeficiente de convecção no desempenho.
Passo 2
Para resolver essa questão, vamos assumir que:
(1) Estamos em condição de estado estacionário;
(2) A transferência de calor é unidimensional;
(3) O chip é isotérmico;
(4) A transferência de calor é desprezível na superfície superior do chip;
(5) O aumento da temperatura do fluxo de ar é desprezível;
(6) O coeficiente de convecção é uniforme associados ao fluxo de ar através dos canais e sobre as superfícies externas do dissipador de calor;
(7) A radiação é desprezível.
A partir dessas considerações podemos começar a resolver a letra (a) onde queremos o valor correspondente da potência do chip a máxima temperatura permitida do chip.
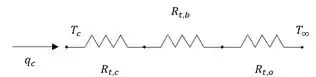
Do circuito térmico, temos:
Onde,
Conhecendo as equações:
, e
Onde,
Passo 3
Tendo,
Então:
Por consequência,
, e
Então:
Passo 4
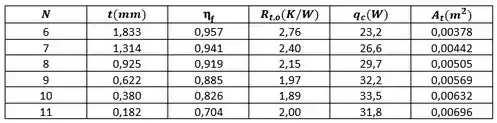
Na letra (b), queremos explorar os efeitos de aumentar a espessura das aletas através da redução do número de aletas e de aumentar o escoamento do ar e assim o coeficiente convectivo. Para o primeiro efeito, podemos gerar a seguinte tabela:
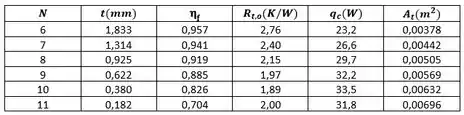
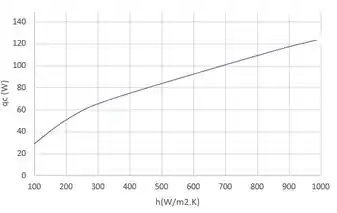
Embora (e ) aumente com a diminuição de (aumento de), há uma redução em que produz um mínimo em , o e, portanto, um valor máximo de , para . Para , o efeito de no desempenho do dissipador de calor é mostrado abaixo.
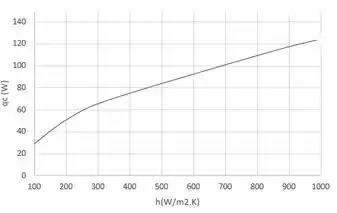
Resposta
(b)
