Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 76

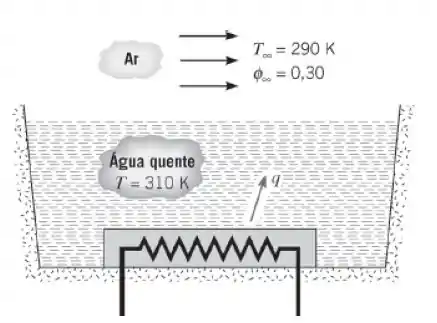
Um bem-sucedido engenheiro californiano instalou em seu jardim uma banheira de hidromassagem circular e avaliou que, para as condições de operação típicas descritas no esboço, a água deve ser reposta a uma taxa de 0,001 k g s de modo a manter o nível de líquido constante na banheira. Sendo os lados e o fundo da banheira isolados termicamente e a temperatura da água de reposição igual à da água que se encontra no interior da banheira,

a qual taxa os aquecedores elétricos devem fornecer energia para manter a temperatura da água na banheira a 310 K?

Passo 1

Faaaaaaaala galerinhaaa !!1

Animados para continuar?

Nós temos que água na hidromassagem está recebendo calor por meio do aquecedor e perdendo calor por convecção e por evaporação:

q " e l - q " e v a p - q " c o n v = 0

Nós podemos abrir um pouquinho o calor, não é?

q " e v a p = n A h f g

q " c o n v = h - A s T s - T ∞

Na fórmula:

q " e l = n A h f g + h - A s T s - T ∞

Vamos ver o que o problema nos disse?

n A = 0,001 k g s

T ∞ = 290   K

T s = 3 1 0 K

Para achar o restante dos nossos valores nós vamos olhar na Tabela A.6:

Como ф ∞ = 0,3 para a temperatura de 290 K:

ρ A ,   ∞ = 0,3 0,0143 k g m 3 = 0,00429 k g m 3

E para a temperatura a 300 K:

ρ A ,   s = 0,0 436 k g m 3

h f g = 24 14 k J k g

Beleza!!! A única coisa que nós não temos é o termo h - A s .

Passo 2

Para isso nós vamos usar uma relação:

h - h m - = ρ c p L e ( 1 - n )

Se nós multiplicarmos a área no denominador e numerador podemos achar o termo que queremos, certo?

h - A s h m A s - = ρ c p L e ( 1 - n )

Onde ρ é a densidade, c p o calor específico a pressão constante, L e o número de Lewis.

O número de Lewis também pode ser escrito como:

L e = α D A B

Onde α é a difusividade térmica e D A B a difusividade mássica!!

Para a maioria das aplicações n = 1 3 :

h - A s h m - A s = ρ c p α D A B 1 - 1 3

h - A s = h m - A s ρ c p α D A B 2 3

Aqui nós precisamos lembrar de algo beem importante:

n A = h m - A s ρ A ,   s - ρ A ,   ∞     →       h m - A s = n A ρ A ,   s - ρ A ,   ∞

Na fórmula:

h - A s = n A ρ c p ρ A ,   s - ρ A ,   ∞ α D A B 2 3

Na Tabela A.4 para nossa temperatura 310 K:

ρ = 1,1 61 k g m 3

c p = 1007 J k g K

α = 22,5 × 10 - 6 m 2 s

E na Tabela A.8 para o vapor de água e o ar para a temperatura da superfície:

D A B = 0,26 × 10 - 4 m 2 s

Substituindo na fórmula para achar a correlação entre os coeficientes:

h - A s = 0,001 k g s 1,161 k g m 3 1007 J k g K 0,0436 k g m 3 - 0,00429 k g m 3 22,5 × 10 - 6 m 2 s 0,26 × 10 - 4 m 2 s 2 3

h - A s = 27 W K

Passo 3

E com tudo isso que nós podemos achar a taxa os aquecedores elétricos

q " e l = 0,001 k g s 2414 × 10 3 J k g + 27 W K 310   K - 290   K

q " e l = 2954   W

Legal, não é ?!

Resposta

q " e l = 2954   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma determinada temperatura e pressão, a difusividade da massa do ar no vapor de água será́ igual à difusividade da massa do vapor de água no ar? Explique.
Como a difusividade de massa da mistura de gases muda com ( a ) a temperatura e ( b ) a pressão?
Como a concentração da substância é definida? Como é definido o gradiente de concentração? Como a taxa de difusão da substância é relacionada com o gradiente de concentração?
Em uma determinada temperatura e pressão, a difusividade da massa do cobre no alumínio será́ igual à difusividade da massa do alumínio no cobre? Explique.
Alguém alega que as frações da massa e molar da mistura dos gases C O 2 e N 2 O são idênticas. Você concorda? Explique.