Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 116

A bomba centrífuga da Figura P3.116 tem um escoamento com vazão Q, saindo do rotor com um ângulo θ 2 , relativo às pás, como mostra a figura. O fluido entra axialmente na seção 1. Considerando escoamento incompressível e velocidade angular ω do eixo constante, deduza uma fórmula para a potência P necessária para acionar o rotor.

Passo 1

Bora que bora que boraaaaa!

Cara, temos um exemplo no livro bem parecido com essa questão, o exemplo 3.14, da uma olhadinha lá também!

Lá, chegamos em uma expressão para o torque, que vai nos ajudar a achar a expressão para a potência, assim:

T 0 = ρ Q r 2 V t 2 - r 1 V t 1   k ^

Assumindo, V t 1 ≈ 0

T 0 = ρ Q r 2 V t 2

Essa expressão considerando um movimento no sentido horário!

Passo 2

Precisaremos de um diagrama de velocidade para continuar, isso porque para encontrar a velocidade de saída absoluta 2, precisaremos adicionar ω r 2 a V r e l , 2 , observe o diagrama:

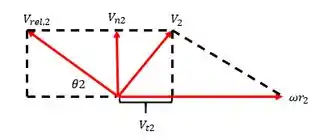
Por trigonometria, chegaremos em:

V t 2 = r 2 ω - V n 2 cot ⁡ θ 2

em que, a velocidade normal é dada por:

V n 2 = Q A s a i d a = Q 2 π r 2 b 2

Passo 3

Sabendo que a potência pode ser dada por, P = ω T , teremos:

P = ρ Q r 2 ω r 2 ω - Q 2 π r 2 b 2 cot ⁡ θ 2

Resposta

P = ρ Q r 2 ω r 2 ω - Q 2 π r 2 b 2 cot ⁡ θ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bomba centrífuga tem pás com ângulo de entrada 15º e de saída de 25º. A rotação é 1720 rpm e os diâmetros de entrada e saída são, respectivamente, de 10cm e 25cm. Sendo v u 1 = 0 e v r 1 = v r 2 ,
No dispositivo da figura, o pistão de peso G = 29,4k N desce muito lentamente dentro do cilindro de área 2m 2 , empurrando a água ( γ = 10 4N / m 3 ) pelos dois cotovelos instalados simetricamente. A
O tampão de base circular da figura está colocado concentricamente na tubulação horizontal de seção circular para controlar a vazão de água. Sendo ρ = 1000k g / m 3 e desprezando a perda de carga, det
Duas bombas recalcam água ( γ = 10 4 N / m 3 ) para o sistema da figura, no qual é lançada na vertical para a atmosfera, na seção 4 . O tubo de saída é isolado do resto da instalação por uma luva elás
Água escoa horizontalmente para fora de um tubo, através de uma fenda de 3m m de largura e 1,8m de comprimento. A vazão é 28L / s e a velocidade varia linearmente desde v m á x á até zero no fim da fe