Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 10
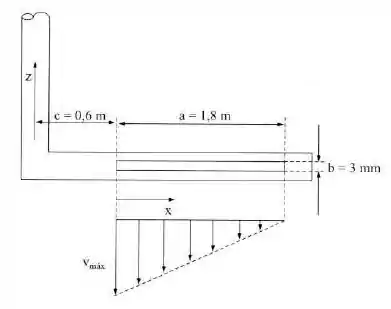
Água escoa horizontalmente para fora de um tubo, através de uma fenda de de largura e de comprimento. A vazão é e a velocidade varia linearmente desde até zero no fim da fenda. Determinar o momento em relação ao eixo vertical, provocado pelo escoamento do fluido .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos aplicar a fórmula do cálculo de momento para tubulações por onde passam fluidos:
Substituindo os valores, temos que:
Resposta
Exercícios de Livros Relacionados
O jato d’água da figura abaixo atinge a placa fixa na normal. Despreze a gravidade e o atrito e calcule a força F, em newtons, necessária para manter a placa fixa.
Água a 20°C escoa em regime permanente através da caixa abaixo, entrando na seção 1 a 2m/s. Calcule (a) a força horizontal e (b) a força vertical necessárias para manter a caixa parada contra o fluxo
Na figura abaixo, a pá fixa desvia o jato d’água em uma meia volta completa. Encontre uma expressão para a velocidade máxima do jato V 0 se a máxima força possível do suporte é F 0 .
Um líquido de massa específica ρ escoa através da contração brusca da figura abaixo e sai para a atmosfera. Considere condições uniformes ( ρ 1 , V 1 , D 1 ) na seção 1 e ( ρ 2 ,V 2 ,D 2 ) na seção 2.
Para o escoamento na redução de seção do tubo da figura abaixo, com D 1 = 8c m , D 2 = 5c m e p 2 = 1a t m . Todos os fluidos estão a 20°C. Se V 1 = 5m / s e a leitura do manômetro é de h = 58c m , ca