Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 16

Uma bomba centrífuga, projetada para bombear água a 1 2 00   r p m , tem dimensões:

R 1 = 90   m m e R 2 = 15 0   m m

b 1 = 10   m m e b 2 = 7,5   m m

β 1 = 25 ° e β 2 = 4 5 °

Determine a vazão para a qual a velocidade de entrada não possui componente tangencial. Trace o diagrama de velocidade de saída e determine o ângulo absoluto do escoamento de saída (medido em relação à direção normal), para esta vazão. Avalie a potência hidráulica fornecida pela bomba, se a sua eficiência for de 70 % . Determine a altura de carga desenvolvida pela bomba.

Passo 1

Diagrama de velocidades para a entrada:

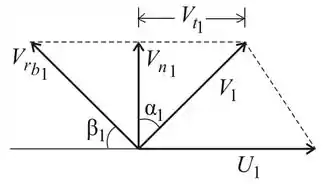
Diagrama de velocidades para a saída:

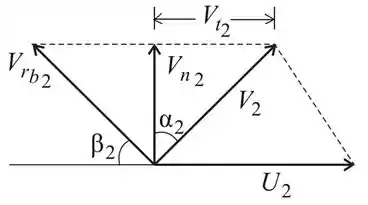
Passo 2

Encontrando a velocidade angular ω :

ω = 2 π N 60

Sendo N a velocidade de 1 2 00   r p m :

ω = 2 π ⋅ 1 2 00 60 = 125,66   r a d / s

Agora, calcularemos as velocidades horizontais de entrada ( U 1 ) e saída ( U 2 ) :

U = R ω

Sendo:

R 1 = 90   m m = 0,0 9   m ;

R 2 = 1 50   m m = 0,1 5   m ;

ω = 125,66   r a d / s .

Temos:

U 1 = 0,0 9 ⋅ 1 25,66 = 11,31   m / s

U 2 = 0,1 5 ⋅ 1 25 , 66 = 18,85   m / s

Passo 3

Calculando V n 1 .

Temos que:

β 1 = tan - 1 ⁡ V n 1 U 1 - V t 1

Como V t 1 = 0 :

β 1 = tan - 1 ⁡ V n 1 U 1

V n 1 = U 1 tan ⁡ β 1

Substituindo os dados:

V n 1 = 11,31 ⋅ tan ⁡ 25 ° = 5,27   m / s

Passo 4

Calculando Q :

A equação de vazão se dá:

Q = 2 π R 1 b 1 V n 1

Substituindo valores temos:

Q = 2 π ⋅ 0,09 ⋅ 0,01 ⋅ 5,27 = 0,0298   m 3 / s

Passo 5

Calculando V n 2 :

Q = 2 π R 2 b 2 V n 2

V n 2 = Q 2 π R 2 b 2

Substituindo os dados conhecidos:

V n 2 = 0,0298 2 π ⋅ 0,15   ⋅ 0,0075 = 4,22   m / s

Passo 6

Calculando a vazão mássica:

m ˙ = ρ Q

Sendo:

ρ = 1000   k g / m 3 ;

Temos:

m ˙ = 1000 ⋅ 0,0298   = 29,80   k g / s

Passo 7

Calculando V t 2 :

V t 2 = U 2 - V n 2 tan ⁡ β 2

V t 2 = 18,85 - 4,22 tan ⁡ 45 ° = 14,63   m / s

Passo 8

Determinando o ângulo absoluto do escoamento de saída.

α 2 = tan - 1 ⁡ V t 2 V n 2

α 2 = tan - 1 ⁡ 14,63   4,22 = 73,91 °

Passo 9

Avaliando a potência hidráulica fornecida pela bomba.

Calcularemos a potência utilizando a equação de turbina de Euler:

W = ( U 2 V t 2 - U 1 V t 1 ) m ˙

Substituindo os dados apresentados anteriormente:

W = 18,85 ⋅ 14,63 - 11,31 ⋅ 0 ⋅ 29,80 = 8,218   k W

Se a sua eficiência for de 70 % :

W f o r n e c i d a = n ⋅ W = 0,70 ⋅ 8,218 = 5,753   k W

Passo 10

Determinando a altura de carga desenvolvida pela bomba.

H = W f o r n e c i d a m ˙ g = 5753 29,80 ⋅ 9,8 = 19,7   m

Resposta

Q = 0,0298   m 3 / s

α 2 = 73,91 °

W f o r n e c i d a = 5,753   k W

H = 19,7   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados de testes de uma bomba operada a 1500r p m , com um rotor de diâmetro 30c m , são:Desenvolva e trace o gráfico de uma equação de ajuste de curva para N P S H Rv e r s u s vazão volumétrica, da f
Curvas típicas de desempenho de uma bomba centrífuga, testada com três diferentes diâmetros de rotor em uma carcaça única são mostradas na figura. Especifique a vazão e a altura de carga produzidas pe
Uma bomba centrífuga opera a 1750r p m ; o rotor tem pás curvadas para trás com β 2 = 60 ° e b 2 = 1,25c m . A uma vazão de 0,025m 3 / s , a velocidade radial de saída é V n 2 = 3,5m / s . Estime a al
No seu ponto de melhor eficiência ( n = 0,85 ) , com D = 400m m , fornece uma vazão de água Q = 1,2m 3 / s a uma altura H = 50m , quando opera a N = 1500r p m . Calcule a velocidade específica desta b
A altura de sucção positiva líquida requerida ( N P S H R ) por uma bomba pode ser expressa aproximadamente como uma função parabólica da vazão em volume. O N P S H R para uma dada bomba, operando a 1